Straight Lines - Test Papers

 CBSE Test Paper 01

CH-10 Straight Lines

---

1. The lines x + 2y – 3 = 0, 2x + y – 3 = 0 and the line l are concurrent . If the line I passes through the origin, then its equation is
   1. x – y = 0
   2. x + y + 0
   3. x + 2y = 0
   4. none of these
2. Projection (the foot of perpendicular) from ( x , y ) on the x – axis is
   1. ( - x , 0 )
   2. ( 0 , y )
   3. ( x , 0 )
   4. ( 0 , - y )
3. The distance of the point (α,β$\alpha ,\beta$) from X axis is
   1. |β|$|\beta |$
   2. |α|$|\alpha |$
   3. none of these.
   4. α$\alpha$
4. A line is drawn through the points ( 3 , 4 ) and ( 5 , 6 ) . If the is extended to a point whose ordinate is – 1, then the abscissa of that point is
   1. none of these
   2. 1
   3. 0
   4. - 2
5. The line which is parallel to X axis and crosses the curve y = x−−√$\sqrt{x}$ at an angle of 450${45}^0$ is:
   1. y = 1/2
   2. y = 1
   3. none of these
   4. y = 14$\frac{1}{4}$
6. Fill in the blanks:

   If a, b, c are in A.P., then the straight line ax + by + c = 0 will always pass through ________.

7. Fill in the blanks:

   The slope of the line, whose inclination is 150o is ________.

8. Prove that the line through the point (x1, y1) and parallel to the line Ax + By + C = 0 is A(x - x1) + B(y - y1) = 0.

9. Prove that the points A (1, 4), B (3, -2) and C (4, - 5) are collinear.

10. Find the equation of the line, where length of the perpendicular segment from the origin to the line is 4 and the inclination of the perpendicular segment with the positive direction of X - axis is 30o.

11. If a, b, c are variables such that 3a + 2b + 4c = 0, then show that the family of lines given by ax + by + c = 0 pass through a fixed point. Also, find the point.

12. Show that the lines 4x + y - 9 = 0, x - 2y + 3 = 0, 5x - y - 6 = 0 make equal intercepts on any line of gradient 2.

13. A line forms a triangle in the first quadrant with the coordinate axes. If the area of the triangle is 543–√$54\sqrt{3}$ sq units and perpendicular drawn from the origin to the line makes an angle 60o with X-axis, then find the equation of the line.

14. Find the equation of the straight lines which passes through the origin and trisect the intercept of line 3x + 4y = 12 between the axes.

15. A rectangle has two opposite vertices at the points (1, 2) and (5,5). If the other vertices lie on the line x = 3, find the equations of the sides of the rectangle.

CBSE Test Paper 01
CH-10 Straight Lines

---

Solution

1. (a) x – y = 0
   Explanation: Equation of a line passing through the intersection of two lies is given by ax1 +by1 +c1 + k(ax2 +by2 +c2) = 0

   Hence x+2y-3 + k(2x+y-3) = 0

   Since it passes through (0,0)

   -3 -3k = 0

   This implies k = -1

   Sustituting for k we get,

   x+2y-3 +(-1)(2x+y-3) = 0

   -x +y =0 or x - y = 0

2. (c) ( x , 0 )
   Explanation: Let L be the foot of the perpendicular from the X axis. Therefore its y coocrdinate is zero

   Therefore the coordiantes of the point L is (x,0)

   Hence option 1 is the correct answer

3. (a) |β|$|\beta |$

   Explanation:
   The distance of a  point from X axis is its y coordinate.
   Hence the distance of the point (α,β$\alpha ,\beta$) from X axis  is |β$\beta$|

4. (d) - 2
   Explanation:

   The slope of the given line is y2−y1x2−x1$\frac{y_2-y_1}{x_2-x_1}$ = 6−45−3$\frac{6-4}{5-3}$ = 1

   Therefore 4−(−1)3−x$\frac{4-(-1)}{3-x}$ = 1
   That is 4+1 = 3 - x
   Therefore x = -2

5. (a) y = 1/2
   Explanation: The equation of the line which is a tangent to the curve y = x−−√$\sqrt{x}$ is 
   y = mx + a/m
   Since it makes and angle of 450, m = 1 
   y2 = x implies a = 1/4
   Hence the equation of the tangent is y = x+

   That is the y intercept is 14−−√$\sqrt{\frac{1}{4}}$ = 1/2
   Hence the equation of the line is y = 1/2

6. (1, -2)

7. −13√$-\frac{1}{\sqrt{3}}$

8. Equation of the line parallel to line Ax + By + C = 0 is Ax + By + K = 0 . . . (i)
   Since line (i) passes through (x1, y1)
   Ax1 + By1 + K = 0...(ii)
   Subtracting (ii) from (i), we have
   A(x - x1) + B(y - y1) = 0

9. Given points are A (1, 4), B (3, -2) and C(4, -5)
   From the condition for collinearity of points A, B and C, we have
   The slope of AB = Slope of BC.
   ∴−2−43−1=−5+24−3$\therefore \frac{-2-4}{3-1}=\frac{-5+2}{4-3}$ [∵ slope =y2−y1x2−x1]$\left[\because \text{ slope }=\frac{y_2-y_1}{x_2-x_1}\right]$
   ⇒$\Rightarrow$ −62=−31⇒−3=−3,$\frac{-6}{2}=\frac{-3}{1}\Rightarrow -3=-3,$ which is true.
   Hence, points A, B and C are collinear.

10. The normal form of the equation of the line is x cos ω$\omega$+ y sinω$\omega$= p
    Given, p = 4, ω$\omega$= 30o. Therefore, the equation of the line is x cos 30o + y sin 30o = 4.
    ⇒x3√2+y12=4⇒3–√x$\Rightarrow x\frac{\sqrt{3}}{2}+y\frac{1}{2}=4\Rightarrow \sqrt{3}x$+ y = 8

11. We have, 3a + 2b + 4c = 0
    ⇒c=−34a−12b$\Rightarrow c=-\frac{3}{4}a-\frac{1}{2}b$
    On substituting this value of c in ax + by + c = 0, we get
    ax+by−34a−12b=0$ax+by-\frac{3}{4}a-\frac{1}{2}b=0$
    ⇒a(x−34)+b(y−12)=0$\Rightarrow a\left(x-\frac{3}{4}\right)+b\left(y-\frac{1}{2}\right)=0$
    ⇒(x−34)+λ(y−12)=0, where λ=ba.$\Rightarrow \left(x-\frac{3}{4}\right)+\lambda \left(y-\frac{1}{2}\right)=0,\text{ where }\lambda =\frac{b}{a}.$
    This equation is of the form L1+λL2=0$L_1+\lambda L_2=0$, which represents a straight line through the intersection of the Line L1 = 0 and L2 = 0 i.e., x−34=0 and y−12=0.$x-\frac{3}{4}=0\text{ and }y-\frac{1}{2}=0.$
    On solving these two equations, we get the point (34,12)$\left(\frac{3}{4},\frac{1}{2}\right)$ which is a fixed point.

12. The equation of any line of gradient 2 is
    y = 2x + c ...(i)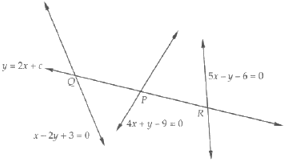
    
    The equations of given lines are
    4x + y - 9 = 0 ...(ii)
    x - 2y + 3 = 0 ...(iii)
    5x - y - 6 = 0 ...(iv)
    Solving (i) with (ii), (iii) and (iv) respectively, we obtain the coordinates of P, Q and R as
    P (32−c6,3+2c3)$\left(\frac{3}{2}-\frac{c}{6},3+\frac{2c}{3}\right)$, Q (1−2c3,2−c3)$\left(1-\frac{2c}{3},2-\frac{c}{3}\right)$ and R (2+c3,4+5c3)$\left(2+\frac{c}{3},4+\frac{5c}{3}\right)$
    Clearly, P is the mid-point of QR. Therefore PQ = PR.
    Hence, lines (ii), (iii) and (iv) make equal intercepts on any line of gradient 2.

13. Since, OM is the perpendicular line on AB.
    Here,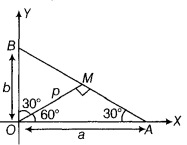 ∠MOB=30∘,∠MOA=60∘$\mathrm{\angle }MOB={30}^{\circ },\mathrm{\angle }MOA={60}^{\circ }$
    
    Let OM = p, OA = a, OB = b
    In ΔOMA,$\mathrm{\Delta }OMA,$
    pa=cos60∘=12⇒a=2p$\frac{p}{a}=\cos {60}^{\circ }=\frac{1}{2}\Rightarrow a=2p$
    In ΔOMB,$\mathrm{\Delta }OMB,$
    pb=cos30∘=3√2⇒b=2p3√$\frac{p}{b}=\cos {30}^{\circ }=\frac{\sqrt{3}}{2}\Rightarrow b=\frac{2p}{\sqrt{3}}$
    ∴ Area of ΔOAB=12×ab=543–√$\therefore \text{ Area of }\mathrm{\Delta }OAB=\frac{1}{2}\times ab=54\sqrt{3}$ [given]
    ⇒12(2p)×(2p)3√=543–√$\Rightarrow \frac{1}{2}(2p)\times \frac{(2p)}{\sqrt{3}}=54\sqrt{3}$
    ⇒4p2=543–√×23–√$\Rightarrow 4p^2=54\sqrt{3}\times 2\sqrt{3}$
    ⇒$\Rightarrow$ p2 = 81 ⇒$\Rightarrow$ p = 9 [∵$\because$ distance is always positive, so we take positive sign]
    Using normal form of the equation of line AB is
    x cosα$\alpha$ + y sinα$\alpha$ = p
    ∴$\therefore$ x cos 60o + y sin60o = 9
    ⇒x(12)+y(3√2)=9$\Rightarrow x\left(\frac{1}{2}\right)+y\left(\frac{\sqrt{3}}{2}\right)=9$
    ⇒x+3–√y−18=0$\Rightarrow x+\sqrt{3}y-18=0$

14. The given line is 3x + 4y = 12 ⇒x4+y3=1$\Rightarrow \frac{x}{4}+\frac{y}{3}=1$ ...(i)
    Let the line (i) cuts X and Y-axes at A and B, respectively.
    Then, A = (4, 0) and B = (0, 3).
    Let the line AB be trisected at P and Q, then
    AP : PB = 1 : 2
    ∴P=(1⋅0+2⋅41+2,1⋅3+2⋅01+2)$\therefore P=\left(\frac{1\cdot 0+2\cdot 4}{1+2},\frac{1\cdot 3+2\cdot 0}{1+2}\right)$
    ⇒P=(83,1)$\Rightarrow P=\left(\frac{8}{3},1\right)$
    and AQ : QB = 2:1
    Also, Q=(2⋅0+1⋅41+2,2⋅3+1⋅02+1)=(43,2)$Q=\left(\frac{2\cdot 0+1\cdot 4}{1+2},\frac{2\cdot 3+1\cdot 0}{2+1}\right)=\left(\frac{4}{3},2\right)$
    Now, equation of line OP passing through (0, 0) and (83,1)$\left(\frac{8}{3},1\right)$ is
    y−0=1−083−0(x−0)⇒y=38x$y-0=\frac{1-0}{\frac{8}{3}-0}(x-0)\Rightarrow y=\frac{3}{8}x$
    ⇒$\Rightarrow$ 3x - 8y = 0
    And equation of the line OQ passing through (0,0) and (43,2)$\left(\frac{4}{3},2\right)$ is
    y−0=2−043−0(x−0)⇒$y-0=\frac{2-0}{\frac{4}{3}-0}(x-0)\Rightarrow$ 2y = 3x ⇒$\Rightarrow$ 3x - 2y = 0

15. Let ABCD be a rectangle whose two opposite vertices are A (1, 2) and C (5,5).
    Let the coordinates of the other two vertices B and D of rectangle ABCD be B (3, y1) and D (3, y2). Since diagonals, AC and BD bisect each other. Therefore, the mid-points of AC and BD are the same.
    ∴$\therefore$ y1+y22=2+52⇒$\frac{y_1+y_2}{2}=\frac{2+5}{2}\Rightarrow$ y1 + y2 = 7 ...(i)
    Since ABCD is a rectangle.
    ∴$\therefore$ AC = BD
    ⇒$\Rightarrow$ AC2 = BD2
    ⇒$\Rightarrow$ (1 - 5)2 + (2 - 5)2 = (3 - 3)2 + (y1 - y2)2
    ⇒$\Rightarrow$ 16 + 9 = (y1 - y2)2
    ⇒$\Rightarrow$ y1 - y2 + ±$\pm$ 5 ....(ii)
    Solving (i) and (ii), we get
    y1 = 6 and y2 = 1 or, y1 = 1 and y2 = 6
    Thus, the coordinates of B and D are B (3,1) and D (3, 6).
    The equation of side AB is
    y - 2 = 1−23−1$\frac{1-2}{3-1}$ (x - 1) or, y - 2 = -12$\frac{1}{2}$ (x - 1) or, x + 2y - 5 = 0
    The equation of side BC is
    y - 1 = 5−15−3$\frac{5-1}{5-3}$ (x - 3) or, y - 1 = 2(x - 3) or, 2x  - y - 5 = 0
    The equation of side CD is
    y - 5 = 6−53−5$\frac{6-5}{3-5}$ (x - 5) or, y - 5 = - 12$\frac{1}{2}$ (x - 5) or, x + 2y -15 = 0
    The equation of side AD is
    y - 2 = 6−23−1$\frac{6-2}{3-1}$ (x - 1) or, y - 2 = 2 (x - 1) or, 2x - y = 0