Conic Sections - Revision Notes

 CBSE Class 11 Mathematics

Revision Notes
Chapter-11
CONIC SECTIONS

---

1. Sections of a Cone, Circle
2. Parabola
3. Ellipse
4. Hyperbola

CIRCLES

• A circle is the set of all points in a plane that are equidistant from a fixed point in the plane.
• The equation of a circle with centre (h, k) and the radius r is(x−h)2+(y−k)2=r2${\left(x-h\right)}^2+{(y-k)}^2=r^2$
• The equation of a circle with centre (0, 0) and the radius r is x2+y2=r2$x^2+y^2=r^2$.
• Characteristics of the equation of a circle:
  (i) Second degree in x$x$ and y$y$.
  (ii) Coefficient of x2$x^2$ = coefficient of y2$y^2$
  (iii) Coefficient of xy$xy$ = 0
• Concentric circles are those circles that have the same centre.
• When ends of diameter are (x1,y1)$\left(x_1,y_1\right)$ and (x2,y2)$\left(x_2,y_2\right)$, then the equaiton of the circle is (x−x1)(x−x2)+(y−y1)(y−y2)=0$\left(x-x_1\right)\left(x-x_2\right)+\left(y-y_1\right)\left(y-y_2\right)=0$
• Position of a point P w.r.t. a circle of radius r$r$ and c$c$ be the centre
  (i) If r>cP,$r>cP,$ point P lies inside the circle.
  (ii) If r=cP,$r=cP,$ point P lies on the circumference of the circle.
  (iii) If r<cP,$r<cP,$ point P lies outside the circle.

PARABOLA

• A parabola is the set of all points in a plane that are equidistant from a fixed line and a fixed point in the plane. In geometric, Parabola is a locus of the point which moves so that its distance from a fixed point is equal to the distance from moving point to a fixed straight line.
• Standard Equation: The equation of the parabola with focus at (a, 0) a > 0 and directrix x = – a is$$   y2 = 4ax.${\text{y}}^2=\text{ 4ax}.$
  
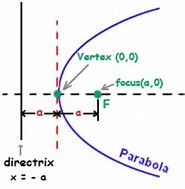
• Focus: The given points are known as Focus.
• Directrix: The fixed straight line is known as Directrix.
• Axis: Any line passing through the focus and perpendicular to the directrix is known as the axis of parabola.
• Vertex: The point of intersection of the axis and the parabola is known as Vertex.
• Latus Rectum: Latus rectum of a parabola is a line segment perpendicular to the axis of the parabola, through the focus and whose end points lie on the parabola.
• Length of the latus rectum of the parabola y2 = 4ax is 4a.${\text{y}}^2=\text{ 4ax is 4a}.$
• Double Ordinate: A chord passing through P (any point on the parabola) and perpendicular to the axis of parabola is called the Double Ordinate through point P.
• Focal Chord: Any chord passing through the focus is known as Focal Chord.
• Four standard forms of Parabola: (i) y2=4ax$y^2=4ax$, (ii) y2=−4ax$y^2=-4ax$, (iii) x2=4ay$x^2=4ay$, (iv) x2=−4ay$x^2=-4ay$.

ELLIPSE

• An Ellipse is the set of all points in a plane, the sum of whose distances from two fixed points in the plane is a constant. If the plane cuts entirely across one nappe of the cone and θ<α<90∘$\theta <\alpha <{90}^{\circ }$, then the curve of intersection of cone and plane is an Ellipse.
• Focus: The fixed point is called the focus and is denoted by F.
• Major Axis: When ellipse is drawn along x−$x-$axis, then the major axis is x−$x-$ and when ellipse is drawn along y−$y-$axis, then the major axis is y−$y-$.
• Distance between focus and centre is denoted by c$c$.
• The equation of an ellipse with focion the x-axis is x2a2+y2b2=1  $\frac{x^2}{a^2}+\frac{y^2}{b^2}=1$
• Relation between a,b,c$a,b,c$ :          c2=a2−b2$c^2=a^2-b^2$
• Latus rectum of an ellipse is a line segment perpendicular to the major axis through any of the foci and whose end points lie on the ellipse.

• Length of the latus rectum of the ellipse x2a2+y2b2=1  is  :2b2a.$\frac{x^2}{a^2}+\frac{y^2}{b^2}=1is:\frac{2b^2}{a}.$

• The eccentricity of an ellipse is the ratio between the distances from the centre of the ellipse to one of the foci and to one of the vertices of the ellipse. Eccentricity:          e=ca$e=\frac{c}{a}$
• Vertical Ellipse: In vertical eelipse, the denominator of y2$y^2$ is greater than x2$x^2$. The equation of this ellipse is x2b2+y2a2=1,$\frac{x^2}{b^2}+\frac{y^2}{a^2}=1,$ where a>b$a>b$.

HYPERBOLA

• A hyperbola is the set of all points in a plane, the difference of whose distances from two fixed points in the plane is a constant.
• Focus: The fixed point is called the focus and is denoted by F.
• Vertex: Point of intersection of hyperbola is called its vertex.

• The equations of a hyperbola with foci on the x-axis is :x2a2−y2b2=1$\frac{x^2}{a^2}-\frac{y^2}{b^2}=1$and y2a2−x2b2=1$\frac{y^2}{a^2}-\frac{x^2}{b^2}=1$
• Distance between two vertices = Lenght of Transverse axis (2a)$(2a)$ and Distance between centre and focus = c$c$
• Relation between a,b,c$a,b,c$ :          c2=a2+b2$c^2=a^2+b^2$
• Conjugate axis: It is a line perpendicular to the transverse axis and passing through the mid-point of two vertices and its length is 2b.$2b.$
• Latus rectum of hyperbola is a line segment perpendicular to the transverse axis through any of the foci and whose end points lie on the hyperbola.

• Length of the latus rectum of the hyperbola :x2a2−y2b2=1  is  :2b2a.$\frac{x^2}{a^2}-\frac{y^2}{b^2}=1is:\frac{2b^2}{a}.$

• The eccentricity of a hyperbola is the ratio of the distances from the centre of the hyperbola to one of the foci and to one of the vertices of the hyperbola. Eccentricity: e=ca