Conic Sections - Solutions
CBSE Class–11 Mathematics
NCERT Solutions
Chapter - 11 Conic Sections
Exercise 11.1
In each of the following Exercises 1 to 5, find the equation of the circle with:
1. Centre (0, 2) and radius 2.
Ans. Given: 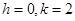 and
and 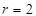
Equation of the circle;
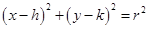
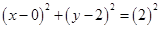

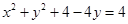

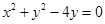
2. Centre 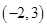 and radius 4.
and radius 4.
Ans. Given: 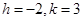 and
and 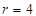
Equation of the circle ;
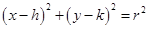
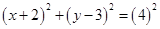

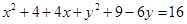

3. Centre 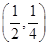 and radius
and radius 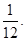
Ans. Given: 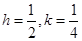 and
and 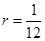
Equation of the circle ;
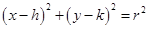
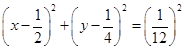

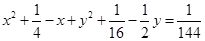

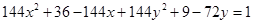

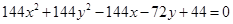

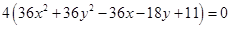

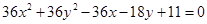
4. Centre 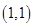 and radius
and radius 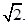
Ans. Given: 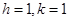 and
and 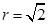
Equation of the circle;
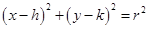
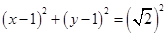

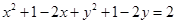

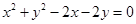
5. Centre 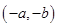 and radius
and radius 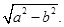
Ans. Given: 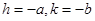 and
and 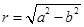
Equation of the circle ;
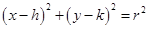
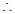
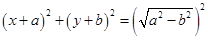

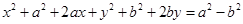

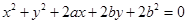
In each of the following Exercises 6 to 9, find the centre and radius of the circles.
6. 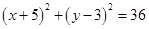
Ans. Given: Equation of the circle;
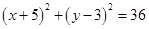

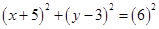 ……….(i)
……….(i)
On comparing eq. (i) with 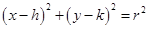
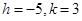 and
and 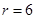
7. 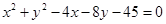
Ans. Given: Equation of the circle: 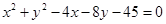

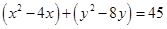

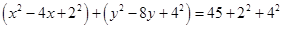
On comparing eq. (i) with 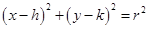
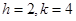 and
and 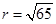
8. 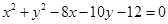
Ans. Given: Equation of the circle;
.......................... (i)
On comparing eq. (i) with
We get, h = 4 , k = 5 and
9. 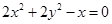
Ans. Given: Equation of the circle: 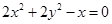

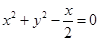 (divide the equation by 2)
(divide the equation by 2)

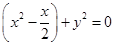

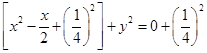
 …….(i)
…….(i)
On comparing eq. (i) with 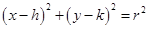
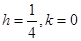 and
and 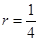
10. Find the equation of the circle passing through the points (4, 1) and (6, 5) and whose centre lies on the line 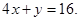
Ans. The equation of the circle is 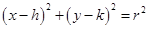 ……….(i)
……….(i)
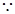 Circle passes through point (4, 1)
Circle passes through point (4, 1)
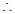
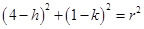

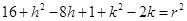

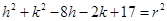 ……….(ii)
……….(ii)
Again Circle passes through point (6, 5)
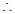
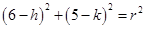

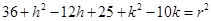

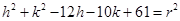 ……….(iii)
……….(iii)
From eq. (ii) and (iii), we have
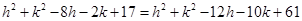

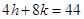

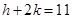 ……….(iv)
……….(iv)
Since the centre 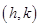 of the circle lies on the line
of the circle lies on the line 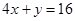
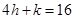 ……….(v)
……….(v)
On solving eq. (iv) and (v), we have 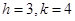
Putting the values of 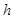 and
and 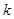 in eq. (ii), we have
in eq. (ii), we have
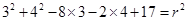

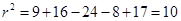
Therefore, the equation of the required circle is
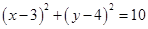

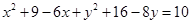

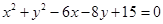
11. Find the equation of the circle passing through the points (2, 3) and 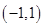 and whose centre lies on the line
and whose centre lies on the line 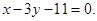
Ans. The equation of the circle is 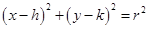 ……….(i)
……….(i)
 Circle passes through point (2, 3)
Circle passes through point (2, 3)
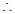
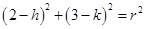

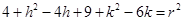

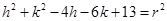 ……….(ii)
……….(ii)
Again Circle passes through point (–1, 1)
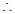
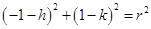

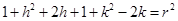

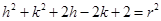 ……….(iii)
……….(iii)
From eq. (ii) and (iii), we have

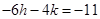

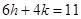 ……….(iv)
……….(iv)
Since the centre 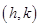 of the circle lies on the line
of the circle lies on the line
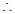
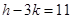 ……….(v)
……….(v)
On solving eq. (iv) and (v), we have 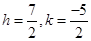
Putting the values of 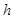 and
and 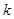 in eq. (ii), we have
in eq. (ii), we have
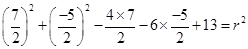

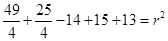

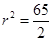
Therefore, the equation of the required circle is
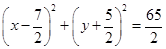

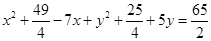

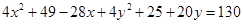

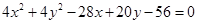

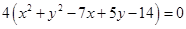

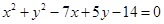
12. Find the equation of the circle with radius 5 whose centre lies on 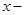 axis and passes through the point (2, 3).
axis and passes through the point (2, 3).
Ans. Since the centre of circle lies on 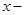 axis, therefore the coordinates of centre is
axis, therefore the coordinates of centre is 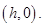
Now the circle passes through the point (2, 3). According to the question,
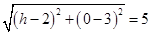

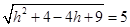

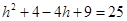

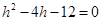

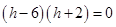

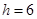 or
or 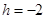
Taking 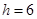 , Equation of the circle is
, Equation of the circle is 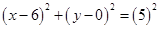

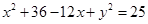

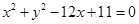
Taking 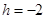 , Equation of the circle is
, Equation of the circle is 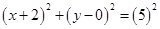

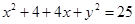

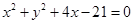
13. Find the equation of the circle passing through (0, 0) and making intercept 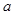 and
and 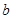 on the coordinate axes.
on the coordinate axes.
Ans. The circle makes intercepts 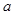 with
with 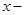 axis and
axis and 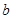 with
with 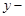 axis.
axis.
 OA =
OA =  and OB =
and OB = 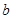
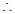 Coordinates of A and B are
Coordinates of A and B are 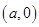 and
and 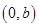 respectively.
respectively.
Now the circle passes through the points O (0, 0), A 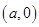 and B
and B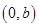 .
.
Putting these coordinates of three points in the equation of the circle,
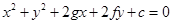 ………(i)
………(i)
Circle passing through (0,0)

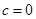
the circle also passes through (a,0) and (0,b)
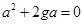

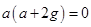

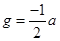
And 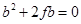

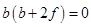

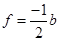
Putting the values of 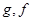 and
and  in eq. (i), we have
in eq. (i), we have
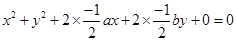

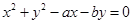
14. Find the equation of the circle with centre (2, 2) and passes through the point
(4, 5).
Ans. The equation of the circle is 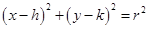 ……….(i)
……….(i)
Since the circle passes through point (4, 5) and coordinates of centre are (2, 2). Radius of circle =
Radius of circle = 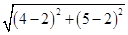 =
= 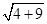 =
= 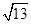
Therefore, the equation of the required circle is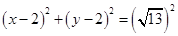

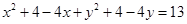

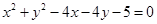
15. Does the point 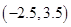 lie inside, outside or on the circle
lie inside, outside or on the circle 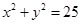 ?
?
Ans. Given: Equation of the circle 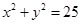

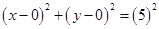
On comparing with 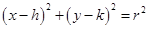 , we have
, we have 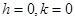 and
and 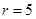
Now distance of the point 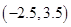 from the centre (0, 0)
from the centre (0, 0)
= 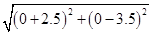 =
= 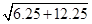 =
= 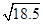 = 4.3 <
= 4.3 <
Therefore, the point 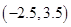 lies inside the circle.
lies inside the circle.