CBSE Class–11 Mathematics
NCERT Solutions
Chapter - 13 Limits and Derivative
Exercise 13.1
Evaluate the following limits in Exercises 1 to 22.
1. 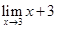
Ans. 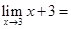 3 + 3 = 6
3 + 3 = 6
2. limx→π(x−227)
Ans. limx→π(x−227)=(π−227)
3. 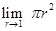
Ans. 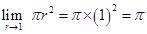
4. 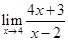
Ans. 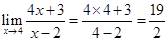
5. 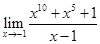
Ans. 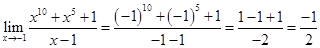
6. 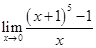
Ans. 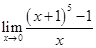 is of the form 00
is of the form 00
Put 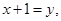 now as
now as 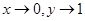
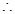 limx→0((x+1)5−1x)= limy→1(y5−1y−1)=limy→1(y5−15y−1)
limx→0((x+1)5−1x)= limy→1(y5−1y−1)=limy→1(y5−15y−1)
=5⋅15−1=5⋅1=5 since limx→a(xn−anx−a)=nan−1
 =5
=5
7. 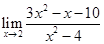
Ans. 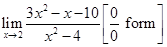
= 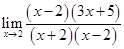
= 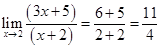
8. 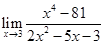
Ans. 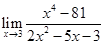 is of the form 00
is of the form 00
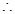
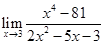 =
=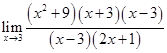
= 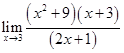
= 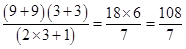
9. 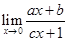
Ans. 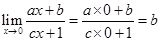
10. 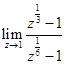
Ans. 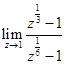 is of the form 00
is of the form 00
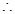
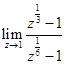 =
= 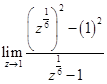
= 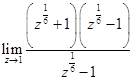
= 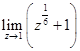
= 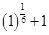 = 1 + 1 = 2
= 1 + 1 = 2
11. 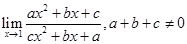
Ans. 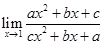
= 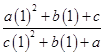
= 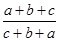 = 1
= 1
12. 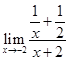
Ans. 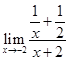 =
= 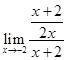
= 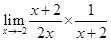
= 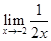 =
= 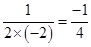
13. 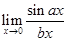
Ans. 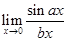
= 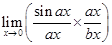
= 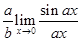
= ablimax→0(sinaxax) [x→0⇒ax→0] and [limθ→0sinθθ=1]
= 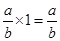
14. 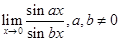
Ans. 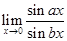
=limx→0(sinaxax)ax(sinbxbx)bx=ablimx→0(sinaxax)(sinbxbx)
=ab⋅limax→0(sinaxax)limbx→0(sinbxbx) since [x→0⇒ax→0x→0⇒bx→0]
= ab⋅11=ab [limθ→0sinθθ=1]
15. 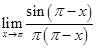
Ans. 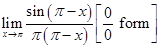
Put 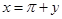 now as
now as 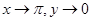
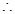
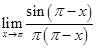 =
= 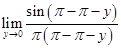
= 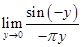 =
= 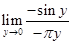 [sin(−θ)=−sinθ]
[sin(−θ)=−sinθ]
= 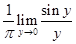 [limθ→0sinθθ=1]
[limθ→0sinθθ=1]
= 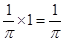
16. 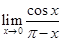
Ans. 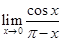 =
= 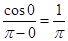
17. 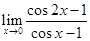
Ans. 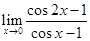 is of the form 00
is of the form 00
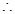 limx→0(cos2x−1cosx−1)=limx→0(2cos2x−1)−1cosx−1 [cos2θ=2cos2θ−1]
limx→0(cos2x−1cosx−1)=limx→0(2cos2x−1)−1cosx−1 [cos2θ=2cos2θ−1]
= limx→02(cos2x−1)cosx−1
= 2limx→0(cosx−1)(cosx+1)(cosx−1)
= 2limx→0(cosx+1)=2(1+1)=2×2=4
18. 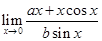
Ans. 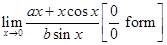
= 1blimx→0x(a+cosx)sinx
= 1blimx→0xsinx⋅limx→0(a+cosx)
= 1b⋅limx→0(a+cosx)limx→0(sinxx) [limθ→0sinθθ=1]
= 1b×a+11=a+1b
19. 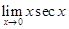
Ans. 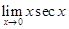 =
= 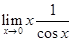
= 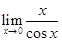 =
= 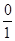 = 0
= 0
20. 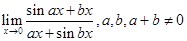
Ans. 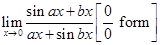
Dividing numerator and denominator by 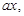
= 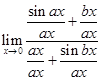
= limx→0(sinaxax)+bxax1+(sinbxbx)bxax
= limax→0(sinaxax)+balim1ax→01+limbx→0(sinbxbx)⋅balimbx→01 [x→0⇒ax→0x→0⇒bx→0]
= 1+ba1+ba=1 [limθ→0sinθθ=1]
21. 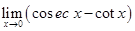
Ans. Given: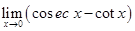
= 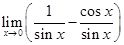 =
= 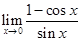
= 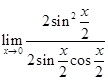 =
= 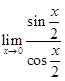
= 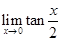 = 0
= 0
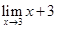
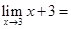 3 + 3 = 6
3 + 3 = 6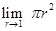
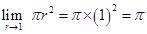
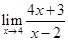
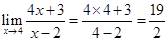
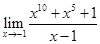
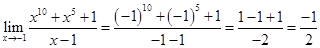
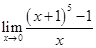
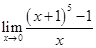 is of the form
is of the form 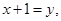 now as
now as 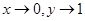
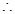 =
= 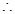
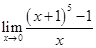 =5
=5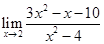
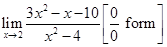
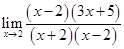
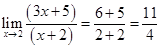
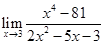
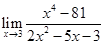 is of the form
is of the form 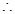
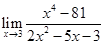 =
=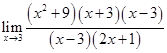
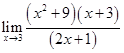
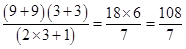
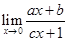
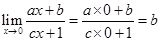
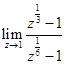
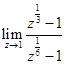 is of the form
is of the form 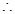
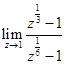 =
= 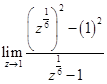
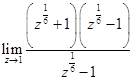
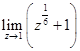
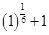 = 1 + 1 = 2
= 1 + 1 = 2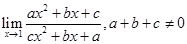
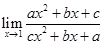
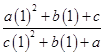
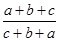 = 1
= 1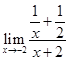
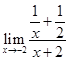 =
= 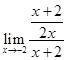
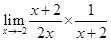
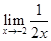 =
= 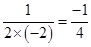
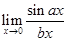
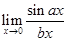
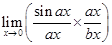
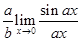
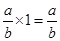
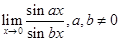
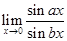
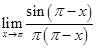
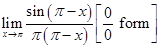
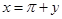 now as
now as 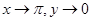
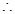
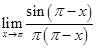 =
= 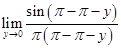
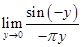 =
= 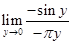
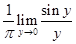
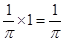
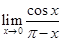
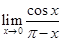 =
= 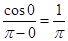
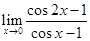
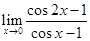 is of the form
is of the form 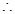
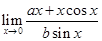
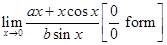
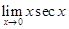
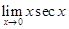 =
= 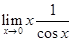
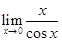 =
= 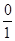 = 0
= 0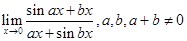
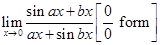
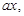
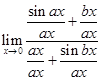
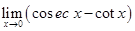
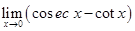
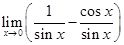 =
= 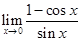
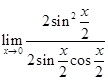 =
= 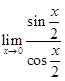
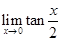 = 0
= 0