Binomial Theorem - Solutions
CBSE Class–11 Mathematics
NCERT Solutions
Chapter - 8 Binomial Theorem
Exercise 8.1
Expand each of the expression in Exercises 1 to 5.
1. 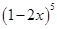
Ans. Using Binomial Theorem,
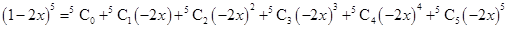
= 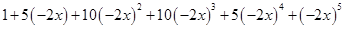
= 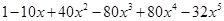 Ans.
Ans.
2. 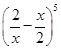
Ans. Using Binomial Theorem,
=
= 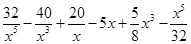
3. 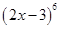
Ans. Using Binomial Theorem,
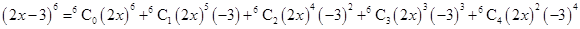
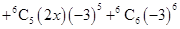
=
= 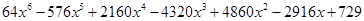
4. 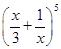
Ans. Using Binomial Theorem,
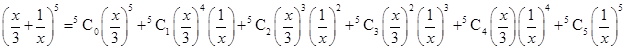
= 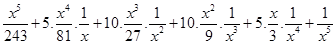
= 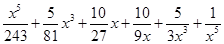
5. 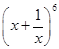
Ans. Using Binomial Theorem,
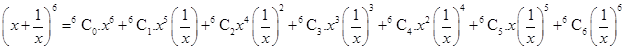
=
= 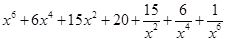
Using binomial theorem evaluate each of the following:
6. 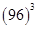
Ans. First we have to express 96 as the sum or difference of two numbers whose powers are easier to calculate and then use Binomial Theorem
We can write
Therefore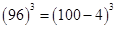
Using Binomial Theorem,
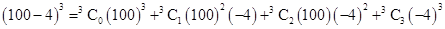
= 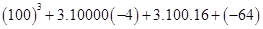
= 1000000 – 120000 + 4800 – 64
= 1004800 – 120064 = 884736
7. 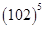
Ans. First we have to express 102 as the sum or difference of two numbers whose powers are easier to calculate and then use Binomial Theorem
We can write 102=100+2
Therefore 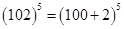
Using Binomial Theorem,
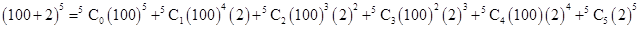
= 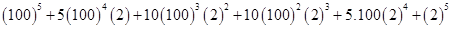
= 10000000000 + 1000000000 + 40000000 + 800000 + 8000 + 32
= 11040808032
8. 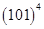
Ans. First we have to express 101 as the sum or difference of two numbers whose powers are easier to calculate and then use Binomial Theorem
We can write 101=100+1
Therefore 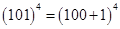
Using Binomial Theorem,
= 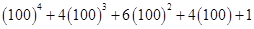
= 100000000 + 4000000 + 60000 + 400 + 1
= 104060401
9. 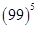
Ans. First we have to express 99 as the sum or difference of two numbers whose powers are easier to calculate and then use Binomial Theorem
We can write
Therefore 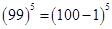
Using Binomial Theorem,
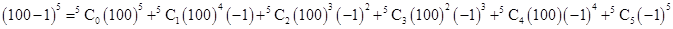 =
=
= 10000000000 – 500000000 + 10000000 – 100000 + 500 – 1
= 9509900499
10. Using binomial theorem, indicate which number is larger 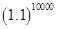 or 1000.
or 1000.
Ans. We have
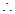
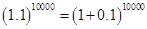
Using Binomial Theorem,
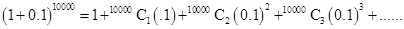
= 1 + 10000 (0.1) + other positive numbers
= 1 + 1000 + other positive numbers
which is greater than 1000
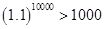
11. Find 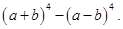 Hence evaluate:
Hence evaluate: 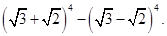
Ans. Given: 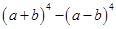
Using Binomial Theorem,
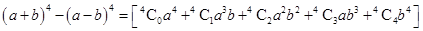
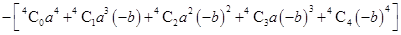
= 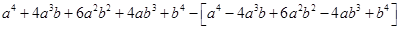
= 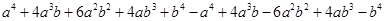
= 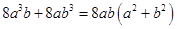
Putting 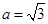 and
and 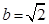
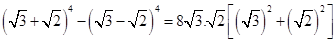
= Ans.
12. Find 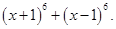 Hence or otherwise evaluate
Hence or otherwise evaluate 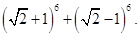
Ans. Given: 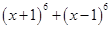
Using Binomial Theorem,
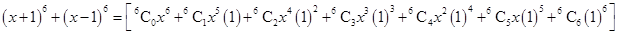
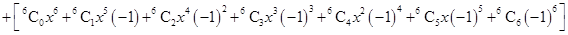
= 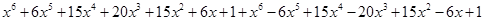
= 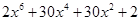 =
= 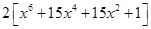
Putting 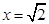
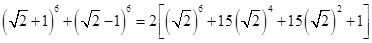
= 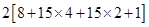
= 2 [ 8 + 60 + 30 + 1] = 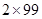 = 198
= 198
13. Show that 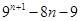 is divisible by 64 whenever
is divisible by 64 whenever 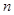 is a positive integer.
is a positive integer.
Ans. We know that b is divisible by a( or a divides b) , k is an integer
Here we have to show that 64 divides 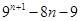
,k is an integer
We have 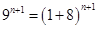
Using Binomial Theorem,we have
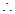
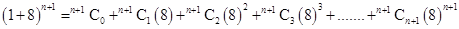
= 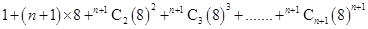
= 
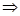
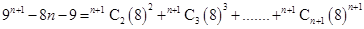
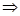
,where is an integer
which shows that 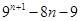 is divisible by 64.
is divisible by 64.
14. Prove that 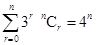
Ans. L.H.S. = 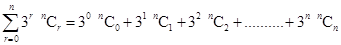
But we have
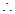
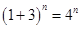
Hence proved