Relations and Functions - Solutions
CBSE Class–11 Mathematics
NCERT Solutions
Chapter - 2 Relations and Functions
Exercise 2.1
1. If 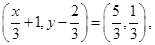 find the values of
find the values of 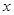 and
and 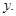
Ans. Here 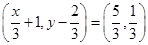
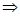
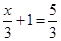 and
and 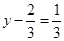
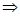
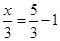 and
and 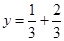
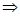
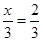 and
and 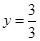
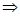
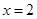 and
and 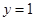
2. If the set A has 3 elements and the set B = {3, 4, 5}, then find the number of elements in (A  B).
B).
Ans. Number of elements in set A = 3 and Number of elements in set B = 3
 Number of elements in A
Number of elements in A  B = 3
B = 3  3 = 9
3 = 9
3. If G = {7, 8} and H = {5, 4, 2}, find G  H and H
H and H  G.
G.
Ans. Given: G = {7, 8} and H = {5, 4, 2}
 G
G H = {(7, 5), (7, 4), (7, 2), (8, 5), (8, 4), (8, 2)}
H = {(7, 5), (7, 4), (7, 2), (8, 5), (8, 4), (8, 2)}
And H  G = {(5, 7), (4, 7), (2, 7), (5, 8), (4, 8), (2, 8)}
G = {(5, 7), (4, 7), (2, 7), (5, 8), (4, 8), (2, 8)}
4. State whether each of the following statements are true or false. If the statement is false, rewrite the given statement correctly:
(i) If P = 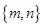 and Q =
and Q = 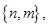 then P
then P  Q =
Q = 
(ii) If A and B are non-empty sets, then A  B is a non-empty set of ordered pairs
B is a non-empty set of ordered pairs 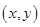 such that
such that 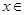 A and
A and 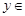 B.
B.
(iii) If A = {1, 2}, B = {3, 4}, then 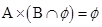
Ans. (i) Here P = 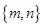 and Q =
and Q = 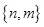
Number of elements in set P = 2 and Number of elements in set Q = 2
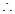 Number of elements in P
Number of elements in P  Q = 2
Q = 2  2 = 4
2 = 4
But P Q =
Q = 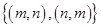 and here number of elements in P
and here number of elements in P  Q = 2
Q = 2
Therefore, statement is false.
Correct statment is
(ii) True
(iii) True
5. If A = 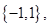 find A
find A  A
A  A.
A.
Ans. Here A = 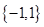
A  A =
A = 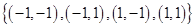
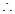 A
A  A
A  A =
A = 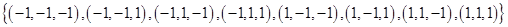
6. If A  B =
B = 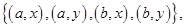 find A and B.
find A and B.
Ans. Given: A  B =
B = 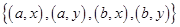
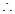 A = set of first elements =
A = set of first elements = 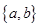 and B = set of second elements =
and B = set of second elements = 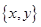
7. Let A = {1, 2}, B = {1, 2, 3, 4}, C = {5, 6} and D = {5, 6, 7, 8}. Verify that:
(i) 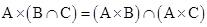
(ii) A  C is a subset of B
C is a subset of B  D.
D.
Ans. Given: A = {1, 2}, B = {1, 2, 3, 4},
C = {5, 6} and D = {5, 6, 7, 8}
(i) 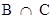 = {1, 2, 3, 4}
= {1, 2, 3, 4} 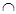 {5, 6} =
{5, 6} = 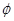
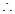
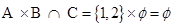 ……….(i)
……….(i)
A  B = {(1, 1), (1, 2), (1, 3), (1, 4), (2, 1), (2, 2), (2, 3), (2, 4)}
B = {(1, 1), (1, 2), (1, 3), (1, 4), (2, 1), (2, 2), (2, 3), (2, 4)}
A  C = {(1, 5), (1, 6), (2, 5), (2, 6)
C = {(1, 5), (1, 6), (2, 5), (2, 6)
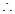 (A
(A B)
B) 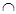 (A
(A  C) =
C) = 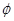 ……….(ii)
……….(ii)
Therefore, from eq. (i) and (ii), 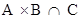
= (A  B)
B) 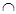 (A
(A  C)
C)
(ii) A  C = {(1, 5), (1, 6), (2, 5), (2, 6)
C = {(1, 5), (1, 6), (2, 5), (2, 6)
B  D = {(1, 5), (1, 6), (1, 7), (1, 8), (2, 5), (2, 6), (2, 7), (2, 8), (3, 5), (3, 6), (3, 7), (3, 8),
D = {(1, 5), (1, 6), (1, 7), (1, 8), (2, 5), (2, 6), (2, 7), (2, 8), (3, 5), (3, 6), (3, 7), (3, 8),
(4, 5), (4, 6), (4, 7), (4, 8),
Therefore, it is clear that each element of A  C is present in B
C is present in B  D.
D.
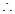 A
A  C
C 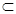 B
B  D
D
8. Let A = {1, 2} and B = {3, 4}, write A  B. How many subsets will A
B. How many subsets will A  B have? List them.
B have? List them.
Ans. Given: A = {1, 2} and B = {3, 4}
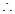 A
A  B = {(1, 3), (1, 4), (2, 3), (2, 4)}
B = {(1, 3), (1, 4), (2, 3), (2, 4)}
Number of elements in A  B = 4
B = 4
Therefore, Number of subsets of A B=24 =16
B=24 =16
,{(2,3)},{(1,4)},{(2,3)},{(2,4)},{(1, 3), (1, 4)} ,{(1, 3),(2, 3)} ,{(1, 3),(2, 4)},{(1, 4), (2, 3)} ,{(1, 4),(2, 4)},{(2, 3), (2, 4)},{(1, 3), (1, 4), (2, 3)} ,{(1, 3), (1, 4), (2, 4)} ,{(1, 3), (2, 3), (2, 4)} ,{(1, 4), (2, 3), (2, 4)},{(1, 3), (1, 4), (2, 3), (2, 4)}
9. Let A and B be two sets such that 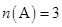 and
and 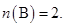 If
If 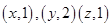 are in A
are in A  B.
B.
Ans. Here 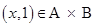
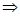
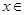 A and
A and 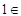 B
B
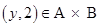
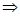
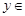 A and
A and 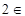 B
B
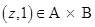
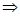
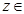 A and
A and 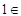 B
B
But it is given that 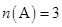 and
and 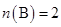
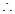 A =
A = 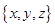 and B = {1, 2}
and B = {1, 2}
10. The Cartesian Product A  A has 9 elements among which are found
A has 9 elements among which are found 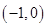 and (0, 1). Find the set A and the remaining elements of A
and (0, 1). Find the set A and the remaining elements of A  A.
A.
Ans. Here 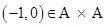
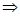
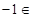 A and
A and 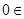 A
A
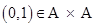
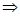
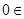 A and
A and 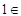 A
A
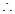
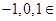 A
A
But it is given that which implies that 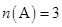
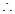 A =
A = 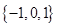
And A  A =
A = 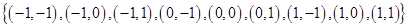
Therefore, the remaining elements of A  A are
A are
(-1,-1), (-1,1), (0,-1), (0,0), (1,-1), (1,0), (1,1)