Principle of Mathematical Induction - NCERT Solutions
CBSE Class–11 Mathematics
NCERT Solutions
Chapter - 4 Principle of Mathematical Induction
Exercise 4.1
Prove the following by using the principle of mathematical induction for all  N:
N:
1. 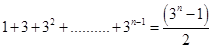
Ans. Let 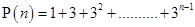
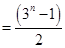
For 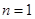

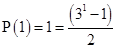
 1 = 1
1 = 1

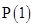 is true.
is true.
Now, let  be true for
be true for 

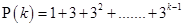
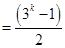 ……….(i)
……….(i)
For 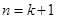

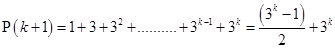 [Using eq. (i)]
[Using eq. (i)]

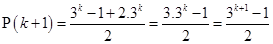

 is true.
is true.
Therefore,  is true.
is true.
Hence by Principle of Mathematical Induction, P(n) is true for all  N.
N.
2. 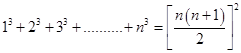
Ans. Let 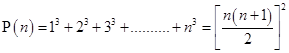
For 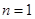

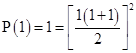
 1 = 1
1 = 1

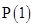 is true.
is true.
Now, let  be true for
be true for 

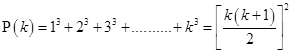 ……….(i)
……….(i)
For 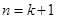
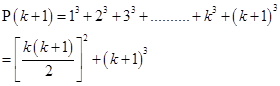

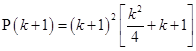
= 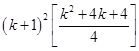
= 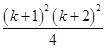

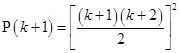

 is true.
is true.
Therefore,  is true.
is true.
Hence by Principle of Mathematical Induction, P(n) is true for all  N.
N.
3. 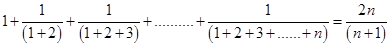
Ans. Let 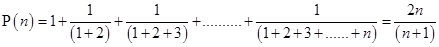
For 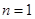

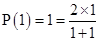
 1 = 1
1 = 1

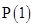 is true.
is true.
Now, let  be true for
be true for 

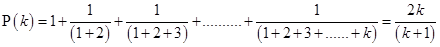 ……….(i)
……….(i)
For 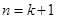

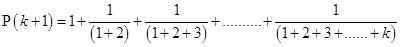
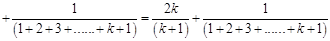 [Using (i)]
[Using (i)]

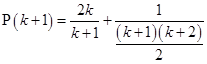
= 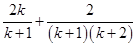
= 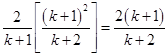

 is true.
is true.
Therefore,  is true..
is true..
Hence by Principle of Mathematical Induction, P(n) is true for all  N.
N.
4. 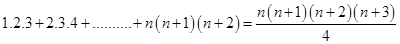
Ans. Let 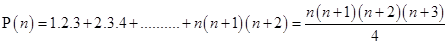
For 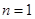

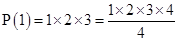
 6 = 6
6 = 6

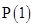 is true.
is true.
Now, let  be true for
be true for 

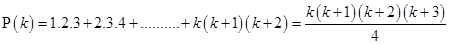 ………(i)
………(i)
For 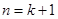

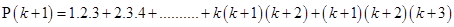
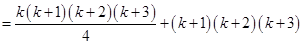 [Using eq. (i)]
[Using eq. (i)]

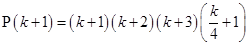
= 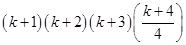

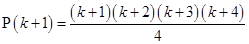

 is true.
is true.
Therefore,  is true.
is true.
Hence by Principle of Mathematical Induction, P(n) is true for all  N.
N.
5. 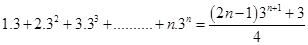
Ans. Let 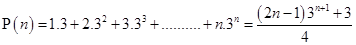
For 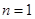

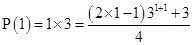
 3 = 3
3 = 3

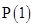 is true.
is true.
Now, let  be true for
be true for 

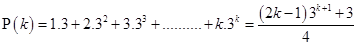
For 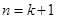

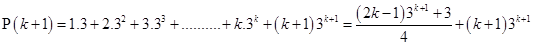

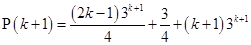
= 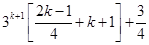

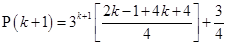
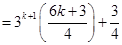

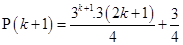
= 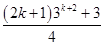

 is true.
is true.
Therefore,  is true.
is true.
Hence by Principle of Mathematical Induction, P(n) is true for all  N.
N.
6. 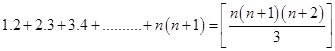
Ans. Let 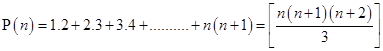
For 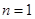

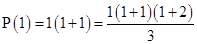
 2 = 2
2 = 2

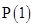 is true.
is true.
Now, let  be true for
be true for 

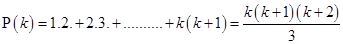 ………(i)
………(i)
For 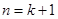

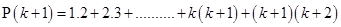
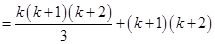

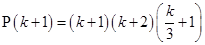
= 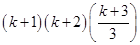
= 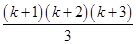

 is true.
is true.
Therefore,  is true.
is true.
Hence by Principle of Mathematical Induction, P(n) is true for all  N.
N.
7. 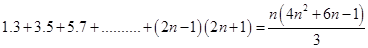
Ans. Let 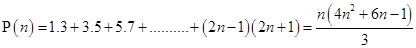
For 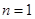
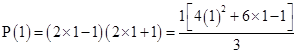
 3 = 3
3 = 3

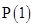 is true.
is true.
Now, let  be true for
be true for 

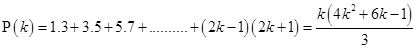
For 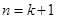
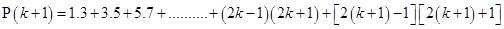
= 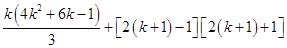

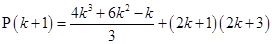
= 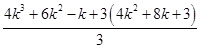

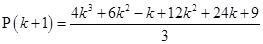
= 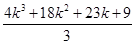
= 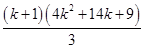

 is true.
is true.
Therefore,  is true.
is true.
Hence by Principle of Mathematical Induction, P(n) is true for all  N.
N.
8. 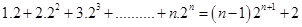
Ans. Let 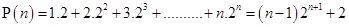
For 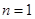
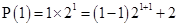
 2 = 2
2 = 2

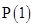 is true.
is true.
Now, let  be true for
be true for 

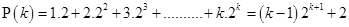
For 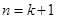
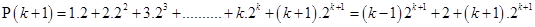

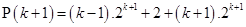
= 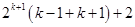
= 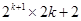 =
= 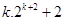

 is true.
is true.
Therefore,  is true.
is true.
Hence by Principle of Mathematical Induction, P(n) is true for all  N.
N.
9. 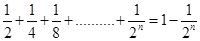
Ans. Let 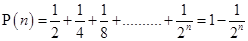
For 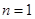
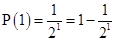

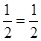
 P(1) is true.
P(1) is true.
Now, let P(n) be true for 

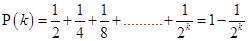
For 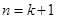

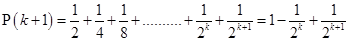

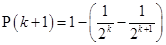
= 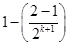 =
= 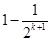

 is true.
is true.
Therefore,  is true.
is true.
Hence by Principle of Mathematical Induction, P(n) is true for all  N.
N.
10. 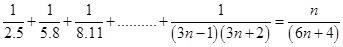
Ans. Let 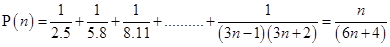
For 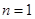

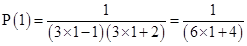

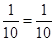

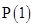 is true.
is true.
Now, let  be true for
be true for 

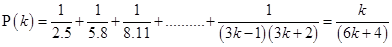
For 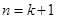

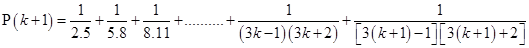


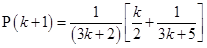
= 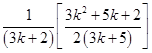
= 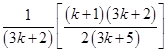

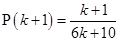

 is true.
is true.
Therefore,  is true.
is true.
Hence by Principle of Mathematical Induction, P(n) is true for all  N.
N.
11. 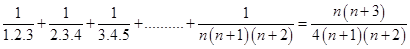
Ans. Let 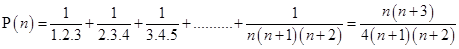
For 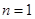

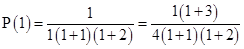

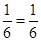

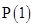 is true.
is true.
Now, let  be true for
be true for 

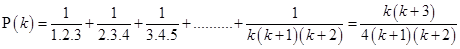 ……….(i)
……….(i)
For 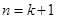
 R.H.S. =
R.H.S. = 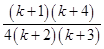
And L.H.S. = 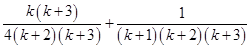 [Using eq. (i)]
[Using eq. (i)]
= 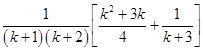
= 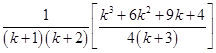
= 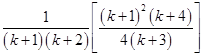
= 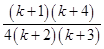

 is true.
is true.
Therefore,  is true.
is true.
Hence by Principle of Mathematical Induction, P(n) is true for all  N.
N.
12. 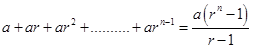
Ans. Let 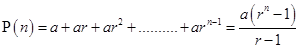
For 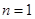

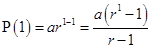

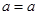

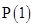 is true.
is true.
Now, let  be true for
be true for 

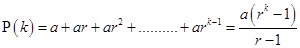 ……….(i)
……….(i)
For 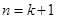
R.H.S. = 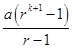
 L.H.S. = [Using eq. (i)]
L.H.S. = [Using eq. (i)]
L.H.S. = 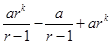
= 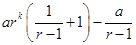
= 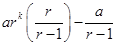
= 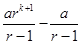
= 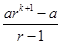
= 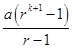

 is true.
is true.
Therefore,  is true.
is true.
Hence by Principle of Mathematical Induction, P(n) is true for all  N.
N.
13. 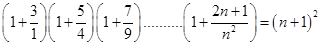
Ans. Let 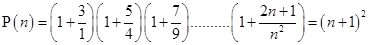
For 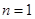
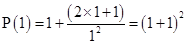

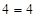

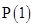 is true.
is true.
Now, let  be true for
be true for 

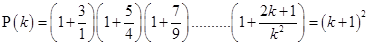 ……….(i)
……….(i)
For 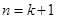
R.H.S. = 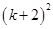
 L.H.S. =
L.H.S. = 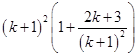 [Using eq. (i)]
[Using eq. (i)]
L.H.S. = 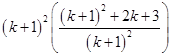
= 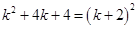

 is true.
is true.
Therefore,  is true.
is true.
Hence by Principle of Mathematical Induction, P(n) is true for all  N.
N.
14. 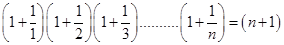
Ans. Let 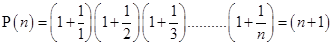
For 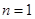
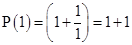

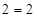

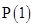 is true.
is true.
Now, let  be true for
be true for 

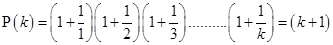
For 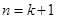
R.H.S. = 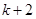
 L.H.S. =
L.H.S. = 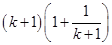 [Using eq. (i)]
[Using eq. (i)]
L.H.S. = 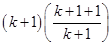 =
= 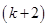

 is true.
is true.
Therefore,  is true.
is true.
Hence by Principle of Mathematical Induction, P(n) is true for all  N.
N.
15. 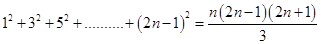
Ans. Let 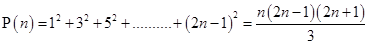
For 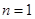

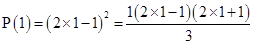

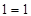

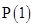 is true.
is true.
Now, let  be true for
be true for 

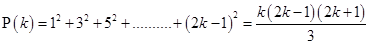 ……….(i)
……….(i)
For 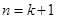
R.H.S. = 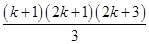
 L.H.S. =
L.H.S. = 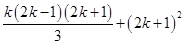 [Using eq. (i)]
[Using eq. (i)]
=
=
= 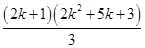
= 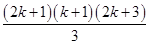
= 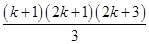

 is true.
is true.
Therefore,  is true.
is true.
Hence by Principle of Mathematical Induction, P(n) is true for all  N.
N.
16. 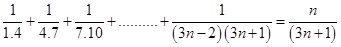
Ans. Let 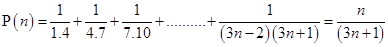
For 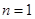

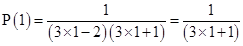

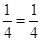

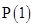 is true.
is true.
Now, let  be true for
be true for 

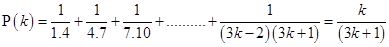 ……….(i)
……….(i)
For 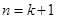
R.H.S. = 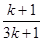
 L.H.S. =
L.H.S. = 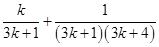
L.H.S. = 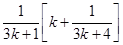
= 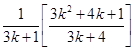
= 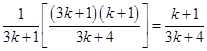

 is true.
is true.
Therefore,  is true.
is true.
Hence by Principle of Mathematical Induction, P(n) is true for all  N.
N.
17. 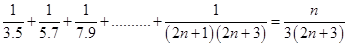
Ans. Let 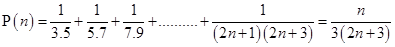
For 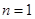

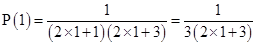

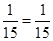

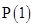 is true.
is true.
Now, let  be true for
be true for 

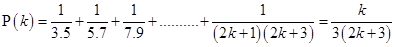 ……….(i)
……….(i)
For 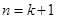
 R.H.S. =
R.H.S. = 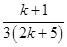
 L.H.S. =
L.H.S. = 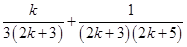
 L.H.S. =
L.H.S. = 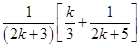
= 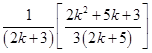
= 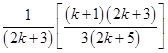
= 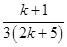

 is true.
is true.
Therefore,  is true.
is true.
Hence by Principle of Mathematical Induction, P(n) is true for all  N.
N.
18. 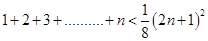
Ans. Let 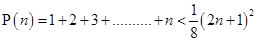
For 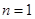

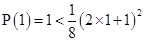

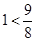

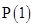 is true.
is true.
Now, let  be true for
be true for 
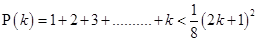 ……….(i)
……….(i)
For 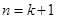 ,
,

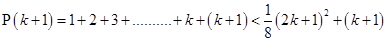
Now, adding 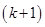 on both sides of eq. (i), we have
on both sides of eq. (i), we have
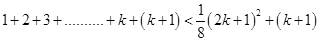

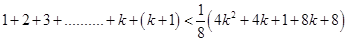

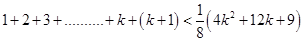

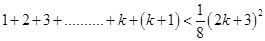

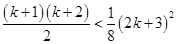

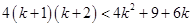

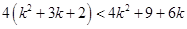

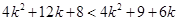
 8 < 9
8 < 9

 is true.
is true.
Therefore,  is true.
is true.
Hence by Principle of Mathematical Induction, P(n) is true for all  N.
N.
19. 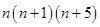 is a multiple of 3.
is a multiple of 3.
Ans. Let 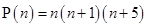 is a multiple of 3.
is a multiple of 3.
For 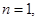

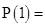 1 (1 + 1) (1 + 5) is a multiple of 3 = 12 is a multiple of 3
1 (1 + 1) (1 + 5) is a multiple of 3 = 12 is a multiple of 3
 P (1) is true.
P (1) is true.
Let  be true for
be true for  ,
,

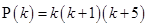 is a multiple of 3.
is a multiple of 3.

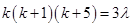

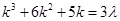

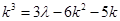 ….(i)
….(i)
For 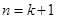 ,
,

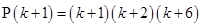 is a multiple of 3
is a multiple of 3
Now, 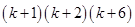
= 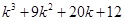
= 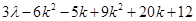 [Using (i)]
[Using (i)]
= 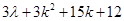
= 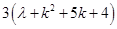
= 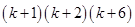 is a multiple of 3
is a multiple of 3

 is true.
is true.
Therefore,  is true.
is true.
Hence by Principle of Mathematical Induction, P(n) is true for all  N.
N.
20. 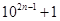 is divisible by 11.
is divisible by 11.
Ans. Let 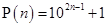 is divisible by 11.
is divisible by 11.
For 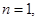
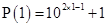 is divisible by 11
is divisible by 11
= 11 is divisible by 11
 P (1) is true.
P (1) is true.
Let  be true for
be true for  ,
,

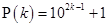 is divisible by 11
is divisible by 11

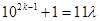

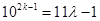 ……….(i)
……….(i)
For 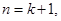

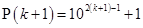 is divisible by 11
is divisible by 11

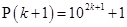 is divisible by 11
is divisible by 11
Now, 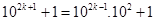
= 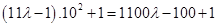
= 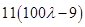

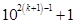 is divisible by 11
is divisible by 11

 is true.
is true.
Therefore,  is true.
is true.
Hence by Principle of Mathematical Induction, P(n) is true for all  N.
N.
21. 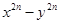 is divisible by
is divisible by 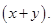
Ans. Let 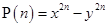 is divisible by
is divisible by 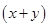
For 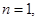

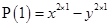 is divisible by
is divisible by 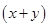

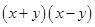 is divisible by
is divisible by 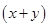
 P (1) is true.
P (1) is true.
Let  be true for
be true for  ,
,

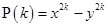 is divisible by
is divisible by 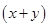

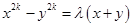

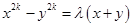 ……….(i)
……….(i)
For 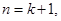

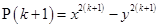 is divisible by
is divisible by 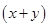
Now,

= 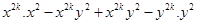
= 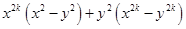
= 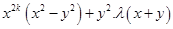 [From eq. (i)]
[From eq. (i)]
= 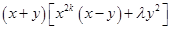

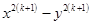 is divisible by
is divisible by 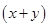

 is true.
is true.
Therefore,  is true.
is true.
Hence by Principle of Mathematical Induction, P(n) is true for all  N.
N.
22. 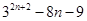 is divisible by 8.
is divisible by 8.
Ans. Let 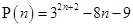 is divisible by 8.
is divisible by 8.
For 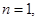

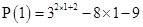 is divisible by 8
is divisible by 8
 64 is divisible by 8
64 is divisible by 8
 P (1) is true.
P (1) is true.
Let  be true for
be true for  ,
,

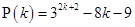 is divisible by 8
is divisible by 8

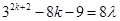

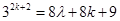 ……….(i)
……….(i)
For 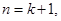

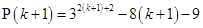 is divisible by 8
is divisible by 8

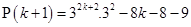 is divisible by 8
is divisible by 8
Now, 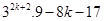
= 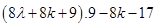 [From eq. (i)]
[From eq. (i)]
= 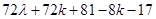
= 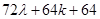

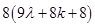

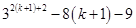 is divisible by 8
is divisible by 8

 is true.
is true.
Therefore,  is true.
is true.
Hence by Principle of Mathematical Induction, P(n) is true for all  N.
N.
23. 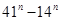 is a multiple of 27.
is a multiple of 27.
Ans. Let 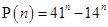 is a multiple of 27.
is a multiple of 27.
For 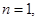
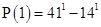 is a multiple of 27
is a multiple of 27
 27 is a multiple of 27
27 is a multiple of 27
 P (1) is true.
P (1) is true.
Let  be true for
be true for  ,
,

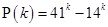 is a multiple of 27
is a multiple of 27

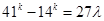 …..(i)
…..(i)
For 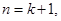

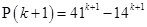 is a multiple of 27
is a multiple of 27
Now, 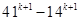
= 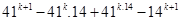
= 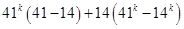
= 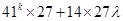 [From eq. (i)]
[From eq. (i)]
= 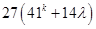

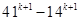 is a multiple of 27
is a multiple of 27

 is true.
is true.
Therefore,  is true.
is true.
Hence by Principle of Mathematical Induction, P(n) is true for all  N.
N.
24. 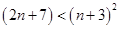
Ans. Let 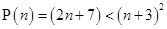
For 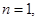
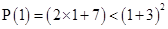
 9 < 16
9 < 16
 P (1) is true.
P (1) is true.
Let  be true for
be true for 
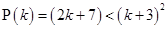 ……….(i)
……….(i)
For 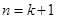
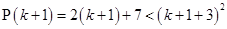
= 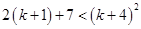
Now, adding 2 on both sides in eq. (i),
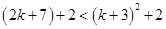

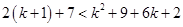

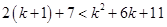

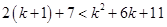
Also 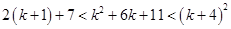

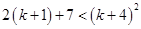

 is true.
is true.
Therefore,  is true.
is true.
Hence by Principle of Mathematical Induction, P(n) is true for all  N.
N.