Linear Inequalities - Test Papers

 CBSE Test Paper 01

CH-06 Linear Inequalities

---

1. The solution set of the inequation 3x <$<$ 5 , when x is a natural number is
   1. { 1,2}
   2. { 1 }
   3. {4 }
   4. { 0,1}
2. The longest side of a triangle is three times the shortest side and the third side is 2cm shorter than the longest side if the perimeter of the triangles at least 61cm, find the minimum length of the shortest side.
   1. 16cm
   2. 61cm
   3. 9cm
   4. 11cm
3. What is the solution set for 2(x−1)5≤3(2+x)7$\frac{2\left(x-1\right)}{5}\le \frac{3\left(2+x\right)}{7}$ ?
   1. [−44,∞)$[-44,\mathrm{\infty })$
   2. (−24,∞)$(-24,\mathrm{\infty })$
   3. (−12,∞)$(-12,\mathrm{\infty })$
   4. (−4,∞)$(-4,\mathrm{\infty })$
4. The graph of the inequalities x ≥ 0 , y ≥ 0 , 2x + y + 6 ≤ 0$\text{x }\ge 0,\text{ y }\ge 0,\text{ 2x }+\text{ y }+\text{ 6 }\le 0$ is
   1. none of these
   2. a triangle
   3. a square
   4. { }
5. − 3x + 17 < − 13$-\text{ 3x }+\text{ 17 }<-\text{ 13}$, then
   1. x∈(−∞,10]$x\in (-\mathrm{\infty },10]$
   2. x∈[10,∞)$x\in [10,\mathrm{\infty })$
   3. none of these
   4. x∈(10,∞)$x\in (10,\mathrm{\infty })$
6. Fill in the blanks:

   If a and b are real numbers, such that a < b, then the set of all real numbers x, such that a < x < b, is called an ________ interval and is denoted by (a, b) or ]a, b[.

7. Fill in the blanks:

   The value of inequality 37 - (3x + 5) ≥$\ge$ 9x - 8(x - 3) is ________.

8. Check whether the given plane 3x - 6y ≤$\le$ 0 contains the point (3, 1).

9. Solve: x5<3x−24−5x−35$\frac{x}{5}<\frac{3x-2}{4}-\frac{5x-3}{5}$

10. Solve: -4x > 30, when

    1. x ∈$\in$ R
    2. x ∈$\in$ Z

11. The cost and revenue functions of a product are given by C (x) = 2x +400 and R(x) = 6x + 20 respectively, where x is the number of items produced by the manufacturer. How many items the manufacturer must sell to realize some profit?

12. Solve the inequalities and show the graph of the solution in case on number line.
    5x−3⩾3x−5$5x-3⩾3x-5$

13. Solve the following system of inequalities graphically: x−2y⩽3$x-2y⩽3$, 3x+4y⩾12$3x+4y⩾12$, x⩾0,y⩾1$x⩾0,y⩾1$

14. Solve the following system of inequalities graphically: x⩾3,y⩾2$x⩾3,y⩾2$

15. Solve for x, |x+3|+xx+2$\frac{|x+3|+x}{x+2}$ > 1

CBSE Test Paper 01
CH-06 Linear Inequalities

---

Solution

1. (b) { 1 }
   Explanation: 3x<5

   ⇒x<53$\Rightarrow x<\frac{5}{3}$

   ⇒x<123$\Rightarrow x<1\frac{2}{3}$

   Hence solution set = {x:x<123,x∈N}={1}$\{x:x<1\frac{2}{3},x\in N\}=\left\{1\right\}$

2. (c) 9cm
   Explanation: Let the shortest side of a triangle be x cm.Then the length of the longest side is3x cm and the length of the third side is (3x-2) cm.
   Given the perimeter of the triangles at least 61cm
   ⇒x+3x+(3x−2)≥61$\Rightarrow x+3x+(3x-2)\ge 61$
   ⇒7x−2≥61$\Rightarrow 7x-2\ge 61$
   ⇒7x≥63$\Rightarrow 7x\ge 63$⇒x≥9$\Rightarrow x\ge 9$

   Hence the minimum length of the shortest side = 9 cm

3. (a) [−44,∞)$[-44,\mathrm{\infty })$

   Explanation:

   Given 2(x−1)5≤3(2+x)7$\frac{2\left(x-1\right)}{5}\le \frac{3\left(2+x\right)}{7}$

   Multiplying both sides by LCM(5,7)=35$\left(5,7\right)=35$,we get
   35.2(x−1)5≤35.3(2+x)7$35.\frac{2(x-1)}{5}\le 35.\frac{3(2+x)}{7}$
   ⇒14(x−1)≤15(2+x)$\Rightarrow 14(x-1)\le 15(2+x)$
   ⇒14x−14≤30+15x$\Rightarrow 14x-14\le 30+15x$
   ⇒14x−15x≤30+14$\Rightarrow 14x-15x\le 30+14$
   ⇒−x≤44$\Rightarrow -x\le 44$
   ⇒x≥−44$\Rightarrow x\ge -44$

   Solution set is [−44,∞)$\left[-44,\mathrm{\infty }\right)$

4. (d) { }
   Explanation:

   We have x ≥ 0⇒2x ≥ 0$\text{x }\ge 0\Rightarrow 2\text{x }\ge 0$

   Also given  y ≥ 0 $\text{ y }\ge 0$

   Hence 2x +y ≥ 0$2\text{x }+\text{y }\ge 0$,which means the minimum value possible for 2x +y $2\text{x }+\text{y }$is  zero.

   Now  2x + y + 6 ≤ 0⇒ 2x + y ≤− 6 $\text{ 2x }+\text{ y }+\text{ 6 }\le 0\Rightarrow \text{ 2x }+\text{ y }\le -\text{ 6 }$  which is not possible 

   Hence  the  system x ≥ 0 , y ≥ 0 , 2x + y + 6 ≤ 0$\text{x }\ge 0,\text{ y }\ge 0,\text{ 2x }+\text{ y }+\text{ 6 }\le 0$ has no solution.

5. (d) x∈(10,∞)$x\in (10,\mathrm{\infty })$

   Explanation:

   − 3x + 17 < − 13$-\text{ 3x }+\text{ 17 }<-\text{ 13}$

   ⇒− 3x + 17 −17< − 13−17$\Rightarrow -\text{ 3x }+\text{ 17 }-17<-\text{ 13}-17$

   ⇒− 3x < − 30$\Rightarrow -\text{ 3x }<-\text{ 30}$

   ⇒−3x−3>−30−3⇒x>10$$\begin{gathered} \Rightarrow \frac{-3x}{-3}>\frac{-30}{-3} \\ \Rightarrow x>10 \end{gathered}$$

   ⇒x∈(10,∞)$\Rightarrow x\in (10,\mathrm{\infty })$

6. open

7. x ≤$\le$ 2

8. We have, 3x - 6y ≤$\le$ 0
   On putting x = 3 and y = 1, we get 3 (3) - 6 (1) ≤$\le$ 0
   ⇒$\Rightarrow$ 9 - 6 ≤$\le$ 0
   ⇒$\Rightarrow$ 3 ≤$\le$ 0, which is not true.
   ∴$\therefore$ the given plane does not contain the point (3, 1).

9. ⇒$\Rightarrow$ x5<3x−24−(5x−3)5$\frac{x}{5}<\frac{3x-2}{4}-\frac{(5x-3)}{5}$
   ⇒$\Rightarrow$  x5<5(3x−2)−4(5x−3)20$\frac{x}{5}<\frac{5(3x-2)-4(5x-3)}{20}$
   ⇒$\Rightarrow$ x < 15x−10−20x+124$\frac{15x-10-20x+12}{4}$
   ⇒$\Rightarrow$ 4x < -5x +2
   ⇒$\Rightarrow$ 4x + 5x < 2
   ⇒$\Rightarrow$ 9x < 2
   ⇒$\Rightarrow$ x < 29$\frac{2}{9}$
   ∴$\therefore$ The solution set is (−∞,29)$\left(-\mathrm{\infty },\frac{2}{9}\right)$

10. Now, -4x > 30
    ⇒x<−304=−152$\Rightarrow x<\frac{-30}{4}=\frac{-15}{2}$

    1. If x ∈$\in$ R, ⇒x∈(−∞,−152)$\Rightarrow x\in \left(-\mathrm{\infty },-\frac{15}{2}\right)$
    2. If x ∈$\in$ Z, ⇒x∈{…,−10,−9−8}$\Rightarrow x\in \{\dots ,-10,-9-8\}$

11. We know that: profit = Revenue - cost. Therefore, to earn some profit, we must have
    revenue > Cost
    ⇒$\Rightarrow$ 6x + 20 > 2x + 400
    ⇒$\Rightarrow$ 6x - 2x > 400 - 20 ⇒$\Rightarrow$ 4x > 380 ⇒$\Rightarrow$ x > 3804$\frac{380}{4}$ = 95
    Hence, the manufacturer must sell more than 95 items to realize some profit.

12. Here 5x−3⩾3x−5$5x-3⩾3x-5$
    ⇒5x−3x⩾−5+3$\Rightarrow 5x-3x⩾-5+3$
    ⇒2x⩾−2$\Rightarrow 2x⩾-2$
    Dividing both sides by 2, we have
    x⩾−1$x⩾-1$
    The solution set is [−1,∞)$\left[-1,\mathrm{\infty }\right)$
    The representation of the solution set on the number line is
    

13. The given inequality is x−2y⩽3$x-2y⩽3$
    Draw the graph of the line x - 2y = 3
    Table of values satisfying the equation x - 2y = 3

    X	1	5
    Y	-1	1

    Putting (0, 0) in the given inequation, we have
    0−2×0⩽3⇒0⩽3$0-2\times 0⩽3\Rightarrow 0⩽3$, which is true.
    ∴$\therefore$ Half plane of x−2y⩽3$x-2y⩽3$ is towards origin.
    Also the given inequality is 3x+4y⩾12$3x+4y⩾12$
    Draw the graph of the line 3x + 4y = 12
    Table of values satisfying the equation 3x + 4y = 12

    X	4	0
    Y	0	3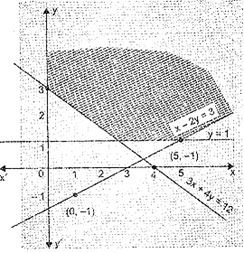

    
    Putting (0, 0) in the given inequation, we have
    3×0+4×0⩾12⇒0⩾12$3\times 0+4\times 0⩾12\Rightarrow 0⩾12$, which is false.
    ∴$\therefore$ Half plane of 3x+4y⩾2$3x+4y⩾2$ is away from origin.
    The given inequality is y⩾1$y⩾1$.
    Draw the graph of the line y = 1.
    Putting (0, 0) in the given inequation, we have
    0⩾1$0⩾1$, which is false.
    ∴$\therefore$ Half plane of y⩾1$y⩾1$ is away from origin.

14. The given inequality is x⩾3$x⩾3$.
    Draw the graph of the line x = 3.
    Putting (0, 0) in the given in equation, we have 0⩾3$0⩾3$ which is false.
    ∴$\therefore$ Half plane of x⩾3$x⩾3$ is away from origin.
    Also the given inequality is y⩾2$y⩾2$
    Draw the graph of the line y = 3.
    Putting (0, 0) in the given inequation, we have 0⩾2$0⩾2$ which is false.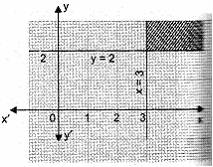
    
    ∴$\therefore$ Half plane of y⩾2$y⩾2$ is away from origin.

15. We have, |x+3|+xx+2$\frac{|x+3|+x}{x+2}$ > 1
    ⇒$\Rightarrow$ |x+3|+xx+2$\frac{|x+3|+x}{x+2}$ - 1 > 0
    ⇒$\Rightarrow$ |x+3|+x−x−2x+2$\frac{|x+3|+x-x-2}{x+2}$ > 0
    ⇒$\Rightarrow$ |x+3|−2x+2$\frac{|x+3|-2}{x+2}$ > 0
    Let x + 3 = 0
    ⇒$\Rightarrow$ x = - 3
    ∴$\therefore$ x = - 3 is a critical point.
    So, here we have two intervals (−∞,−3)$(-\mathrm{\infty },-3)$ and [−3,∞)$[-3,\mathrm{\infty })$
    Case I: When - 3 ≤$\le$ x < ∞$\mathrm{\infty }$, then |x+3|$|x+3|$= (x + 3)
    ∴$\therefore$ |x+3|−2x+2$\frac{|x+3|-2}{x+2}$ > 0
    ⇒$\Rightarrow$ x+3−2x+2$\frac{x+3-2}{x+2}$ > 0
    ⇒$\Rightarrow$ x+1x+2$\frac{x+1}{x+2}$ > 0
    ⇒$\Rightarrow$ (x+1)(x+2)2(x+2)$\frac{(x+1)(x+2{)}^2}{(x+2)}$ > 0 ×$\times$ (x + 2)2
    ⇒$\Rightarrow$ (x + 1) (x + 2) > 0
    Product of (x + 1) and (x + 2) will be positive, if both are of same sign.
    ∴$\therefore$ (x + 1) > 0 and (x + 2) > 0 or (x + 1) < 0 and (x + 2) < 0
    ⇒$\Rightarrow$ x > - 1 and x > - 2 or x < - 1 and x < - 2
    On number line, these inequalities can be represented as,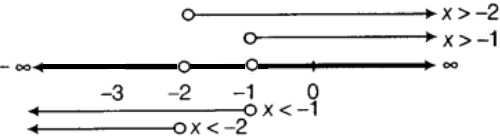
    
    Thus, - 1 < x < ∞$\mathrm{\infty }$ or - ∞$\mathrm{\infty }$ < x < - 2
    But, here - 3 ≤$\le$ x < ∞$\mathrm{\infty }$
    ∴$\therefore$ - 1 < x < ∞$\mathrm{\infty }$ or - 3 ≤$\le$ x < - 2
    Then, solution set in this case is
    x∈$x\in$ [- 3, - 2) ∪$\cup$ (- 1, ∞$\mathrm{\infty }$)
    Case II: When x < - 3, then |x+3|$|x+3|$ = - (x + 3)
    ∴$\therefore$ |x+3|−2x+2$\frac{|x+3|-2}{x+2}$ > 0
    ⇒$\Rightarrow$ −x−3−2x+2$\frac{-x-3-2}{x+2}$ > 0
    ⇒$\Rightarrow$ −(x+5)x+2$\frac{-(x+5)}{x+2}$ > 0
    ⇒$\Rightarrow$ x+5x+2$\frac{x+5}{x+2}$ < 0
    ⇒$\Rightarrow$ (x+5)(x+2)2x+2$\frac{(x+5)(x+2{)}^2}{x+2}$ < 0 ×$\times$ (x + 2)2 
    ⇒$\Rightarrow$ (x + 5) (x + 2) < 0
    Product of (x + 5) and (x + 2) will be negative, if both are of opposite sign.
    ∴$\therefore$ (x + 5) > 0 and (x + 2) < 0 or (x + 5) < 0 and (x + 2) > 0
    ⇒$\Rightarrow$ x > - 5 and x < - 2 or x < - 5 and x > - 2
    On number line, these inequalities can be represented as,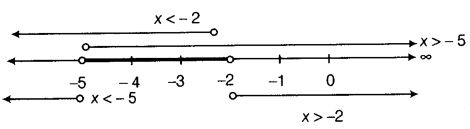
    
    Thus, - 5 < x < - 2 i.e., solution set in the case is x∈$x\in$ (- 5, - 2).
    On combining cases I and II, we get the required solution set of given inequality, which is  x∈$x\in$ (- 5, - 2) ∪$\cup$ ( - 1, ∞$\mathrm{\infty }$)