Linear Inequalities - Solutions

 CBSE Class–11 Mathematics

NCERT Solutions
Chapter - 6 Linear Inequalities
Exercise 6.1

---

1. Solve  24x < 100  when:

(i) x is a natural number

(ii) x is an integer

Ans. Given: 24x < 100 

Divide both sides by 24,

=>24x24<10024$=>\frac{24x}{24}<\frac{100}{24}$

=>x<256$=>x<\frac{25}{6}$

(i) When x is a natural number then values of x that make statement true are 1, 2, 3, 4. The solution set of inequality is {1, 2, 3, 4}.

(ii) When x is an integer, then values of x that make statement true for all ( -ve number and 0,1,2,3,4). So, The solution set of inequality is {......,-4,-3 - 2, - 1,0,1,2,3,4}.

---

2. Solve  -12x > 30 when:

(i)   x is a natural number

(ii)  x is an integer

Ans. Given: -12x >30

Divide both sides by −12$-12$ , then we get,

=>−12x−12<30−12$=>\frac{-12x}{-12}<\frac{30}{-12}$

=>x<−52$=>x<-\frac{5}{2}$

(i) There is no natural number less than −52$-\frac{5}{2}$, so when x is natural number , there is no solution for the given inequality.

(ii) When x is an integer then values of x that make statement true for {............,-5, -4, -3}.  The solution set of inequality is {............,-5, -4, -3}

---

2. Solve  when:

(i) 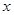 is a natural number

(ii) 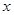 is an integer

Ans. Given: 

Dividing both sides by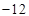 

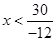
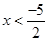
(i) When 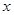 is a natural number then values of  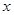that make statement true are none.

(ii) When 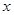 is an integer then values of  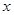that make statement true are  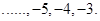The solution set of inequality is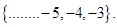 

---

3. Solve 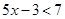 when

(i) 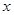 is an integer

(ii) 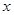 is a real number

Ans. Given: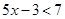 

 

 

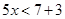
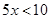
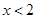
(i) When 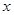 is an integer then values of  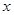that make statement true are  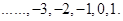The solution set of inequality is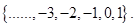 

(ii) When 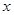 is a real number then solution set of inequality is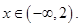 

---

4. Solve  when:

(i) 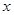 is an integer

(ii) 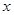 is a real number

Ans. Given: 

 

 

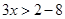
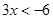
(i) When 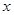 is an integer then values of  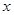that make statement true are  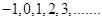The solution set of inequality is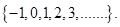 

(ii) When 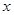 is a real number then solution set of inequality is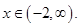 

---

Solve the inequalities in Exercises 5 to 16 for real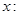 

5. 

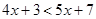
Ans. Here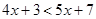 

 

 

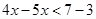
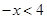
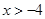
Therefore, the solution set is 

---

6. 

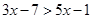
Ans. Here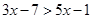 

 

 

 

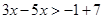
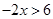
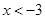
Therefore, the solution set is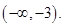 

---

7. 

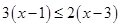
Ans. Here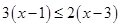 

 

 

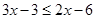
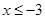
Therefore, the solution set is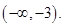 

---

8. 

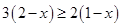
Ans. Here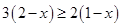 

 

 

 

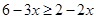
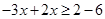
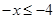
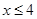
Therefore, the solution set is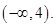 

---

9. 

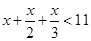
Ans. Here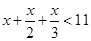 

 

 

 

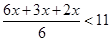
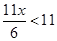
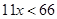
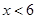
Therefore, the solution set is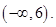 

---

10. 

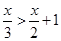
Ans. Here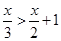 

 

 

 

 

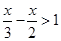
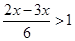
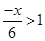
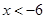
Therefore, the solution set is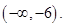 

---

11. 

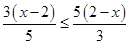
Ans. Here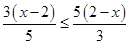 

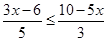
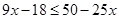
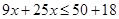
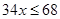
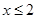
Therefore, the solution set is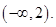 

---

12. 

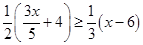
Ans. Here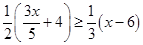 

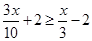
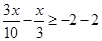
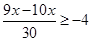
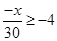
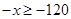
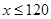
Therefore, the solution set is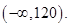 

---

13. 

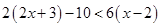
Ans. Here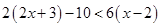 

 

 

 

 

 

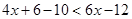
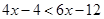
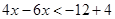
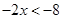
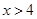
Therefore, the solution set is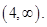 

---

14. 

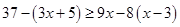
Ans. Here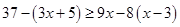 

 

 

 

 

 

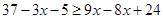
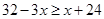
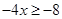
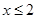
Therefore, the solution set is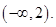 

---

15. 

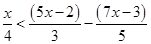
Ans. Here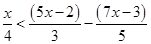 

 

 

 

   

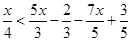
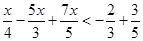
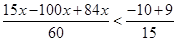
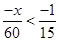
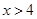
Therefore, the solution set is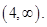 

---

16. 

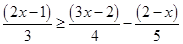
Ans. Here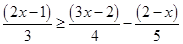 

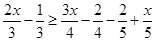
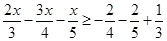
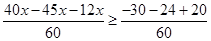
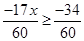
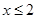
Therefore, the solution set is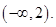 

---

Solve the inequalities in Exercises 17 to 20 and show the graph of the solution in each case on number line:

17. 

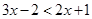
Ans. Here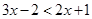 

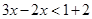
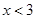
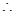The solution set is 

---

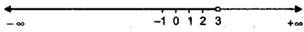
18. 

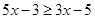
Ans. Here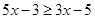 

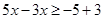
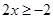
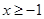
The solution set is 

---

19. 

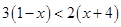
Ans. Here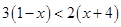 

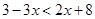
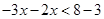
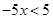
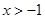
The solution set is 

---

20. 

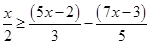
Ans. Here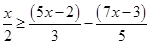 

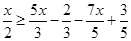
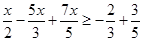
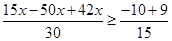
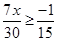
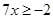
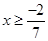
The solution set is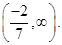 

---

21. Ravi obtained 70 and 75 marks in first two unit tests. Find the minimum marks he should get in the third test to have an average of at least 60 marks.

Ans. Let the marks obtained by Ravi in third test be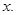 

According to question,

 

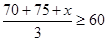
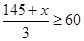
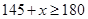
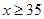
Therefore, minimum marks needed to be obtained by Ravi is 35.

---

22. To receive Grade ‘A’ in a course, one must obtain an average 90 marks or more in five examinations (each of 100 marks). If Sunita’s marks in first four examinations are 87, 92, 94 and 95, find minimum marks that Sunita must obtain in fifth examination to get Grade ‘A’ in the course.

Ans. Let the marks obtained by Sunita in fifth examination be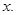 

According to question,

 

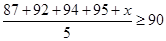
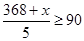
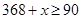
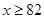
Therefore, minimum marks needed to be obtained by Sunita is 82.

---

23. Find all pairs of consecutive odd positive integers both of which are smaller than 10 such that their sum is more than 11.

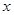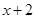Ans. Let  and  be two consecutive odd positive integers.

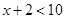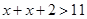
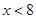and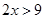 

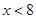 and 

 and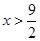 

 

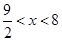
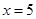  and 7

Therefore, the required pairs of odd positive integers are (5, 7) and (7, 9).

---

24. Find all pairs of consecutive even positive integers, both of which are larger than 5 such that their sum is less than 23.

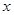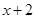Ans. Let  and  be two consecutive even positive integers.

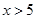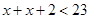
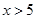 and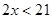 

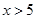 and 

 and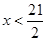 

 

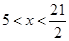
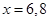  and 10

Therefore, the required pairs of even positive integers are (6,8), (8 10) and (10, 12).

---

25. The longest side of a triangle is 3 times the shortest side and the third side is 2 cm shorter than the longest side. If the perimeter of the triangle is at least 61 cm. Find the minimum length of the shortest side

Ans. Let the length of the shortest side be 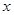 cm.

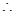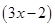Length of longest side =  cm and length of third side =  cm

Perimeter of triangle = 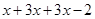 =  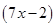cm

Now,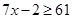 

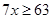
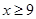
Therefore, the minimum length of shortest side is 9 cm.

---

26. A man wants to cut three lengths from a single piece of board of length 91 cm. The second length is to be 3 cm longer than the shortest and the third length is to be twice as long as the shortest. What are the possible lengths of the shortest board if the third piece is to be at least 5 cm longer than the second?

Ans. Let the length of the shortest side be 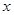 cm.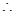
Length of the second board =  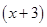cm and length of third side =  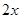cm
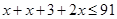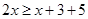
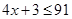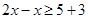
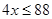Now,  and 
 and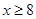 
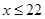 and 
 and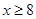 
Therefore, minimum length of shortest board is 8 cm and maximum length is 22 cm.