Introduction to 3D Geometry - Test Papers

 CBSE Test Paper 01

CH-12 Three Dimensional Geometry

---

1. The locus of the equation xy + yz = 0 is
   1. a pair of straight lines
   2. a pair of parallel planes
   3. none of these
   4. a pair of perpendicular planes
2. The coordinates of the point which divides the line segment joining the points ( 5 , 4, 2 ) and ( - 1 , - 2 , 4 ) in the ratio 2 : 3 externally is
   1. ( 17 , 16 , -2 )
   2. none of these
   3. ( 13/5 , 8/5 , 14/5 )
   4. ( 17/5 , 16/5 , - 2/5 )
3. Skew lines are
   1. intersecting lines
   2. parallel lines
   3. coplanar lines
   4. none of these
4. The points ( 1, 2 , 3 ) , ( - 1, -1 , - 1 ) and ( 3, 5 , 7 ) are the vertices of
   1. a right triangle
   2. none of these
   3. an equilateral triangle
   4. an isosceles triangle
5. The number of spheres of a given radius r and touching the coordinate axes is
   1. none of these
   2. 6
   3. 8
   4. 4
6. Fill in the blanks:

   L is the foot of perpendicular drawn from the point P(3, 4, 5) on zx-planes. The coordinates of L are ________

7. Fill in the blanks:

   The coordinates of a point are the perpendicular distance from the ________ on the respectives axes.

8. L is the foot of the perpendicular drawn from a point P(3,4,5) on the XY-plane. Find the coordinates of point L.

9. A point is on the XZ-plane. What can you say about its y-coordinate?

10. If A (- 2, 2, 3) and B (13, - 3,13) are two points. Find the locus of a point P which moves in such a way that 3PA = 2PB.

11. A( 1, 2, 3), B (0, 4,1), C (-1, -1, - 3) are the vertices of a triangle ABC. Find the point in which the bisector of the angle ∠$\mathrm{\angle }$ BAC meets BC.

12. Find the coordinates of centroid of the △ABC$\mathrm{△}ABC$, whose vertices are A (x1, y1, z1), B (x2, y2, z2) and C(x3, y3, z3).

13. Find the equation of the set of the point P, the sum of whose distance from A(4, 0, 0) and B(-4, 0, 0) is equal to 10.

14. Find a point in XY plane which is equidistant from three points (2, 0, 3), (0, 3, 2) and (0, 0, 1).

15. Show that the points (-2, 6, -2), (0, 4, -1), (-2,3,1) and (-4,5,0) are the vertices of a square.

CBSE Test Paper 01
CH-12 Three Dimensional Geometry

---

Solution

1. (d) a pair of perpendicular planes
   Explanation: xy represents the plane through origin and perpendicular to z axis.Similarly yz represents the plane through origin and perpendicular to x axis.hence it represents pair of perpendicular lines
2. (b) none of these
   Explanation: for external division ration must be greater than 1
3. (d) none of these
   Explanation: Skew lines are those lines which lie in different planes and never meet
4. (b) none of these
   Explanation: Let A= ( 1, 2 , 3 ) ,B = ( - 1, -1 , - 1 ) and  C= ( 3, 5 , 7)
   By distance formula between two points (x1, y1, z1) and (x2, y2, z2) = 
   (x1−x2)2+(y1−y2)2+(z1−z2)2−−−−−−−−−−−−−−−−−−−−−−−−−−−−√$\sqrt{{(x1-x2)}^2+{(y1-y2)}^2+{(z1-z2)}^2}$
   we get AB = 29−−√$\sqrt{29}$ , BC = 116−−−√$\sqrt{116}$ = 229−−√$\sqrt{29}$
   AC= 29−−√$\sqrt{29}$
   As we know triangle is possible only if sum of any two sides is greater than 3rd but in our case this condition is not holding so traingle is not possible. these are collinear points
5. (c) 8
   Explanation: Each octant will have one sphere of radius r touching axes. So there are 8 such spheres.

6. (3, 0, 5)

7. given point

8. Since, in an XY-plane, the z-coordinate will be zero. Hence, the coordinate of the point L(3, 4, 0) in XY-plane.

9. We know that coordinates of any point in XZ-plane will be (x, 0, z). Thus y-coordinate of the point is zero.

10. Let P be (x,y, z). Here A(−2,2,3) and B(13,−3,13)
    Now, 3PA = 2PB
    ⇒$\Rightarrow$ 3(x+2)2+(y−2)2+(z−3)2−−−−−−−−−−−−−−−−−−−−−−−√$3\sqrt{(x+2{)}^2+(y-2{)}^2+(z-3{)}^2}$ = 2(x−13)2+(y+3)2+(z−13)2−−−−−−−−−−−−−−−−−−−−−−−−−√$2\sqrt{(x-13{)}^2+(y+3{)}^2+(z-13{)}^2}$ 
    ⇒$\Rightarrow$ 9[x2 + 4x + 4 + y2 + 4 − 4y + z2 + 9 − 6z] = 4[x2 + 169 − 26x + y2 + 9 + 6y + z2 + 169 − 26z] (Squaring both the sides)
    ⇒$\Rightarrow$ 9 [x2 + y2 + z2 + 4x - 4y - 6z + 17] - 4 [x2 - 26x + y2 + 6y + z2 - 26z + 347] = 0
    ⇒$\Rightarrow$ 5x2 + 5y2 + 5z2 + 140x − 60y + 50z − 1235 = 0
    ⇒$\Rightarrow$ 5(x2 + y2 + z2) + 140x − 60y + 50z − 1235 = 0

11. Given points: A(1, 2, 3), B(0, 4, 1), C(−1, −1, −3)
    Angle bisector divides BC in ratio of AB:AC
    AB = (0−1)2+(4−2)2+(1−3)2−−−−−−−−−−−−−−−−−−−−−−−√$\sqrt{(0-1{)}^2+(4-2{)}^2+(1-3{)}^2}$ =1+4+4−−−−−−−√=3$\sqrt{1+4+4}=3$
    AC = (−1−1)2+(−1−2)2+(−3−3)2−−−−−−−−−−−−−−−−−−−−−−−−−−−√$\sqrt{(-1-1{)}^2+(-1-2{)}^2+(-3-3{)}^2}$=4+9+36−−−−−−−−√$\sqrt{4+9+36}$ = 7
    Assume D divides BC in ratio,
    m:n = AB:AC = 3:7
    So D = (3(−1)+7(0)3+7,3(−1)+7(4)3+7,3(−3)+7(1)3+7)$\left(\frac{3(-1)+7(0)}{3+7},\frac{3(-1)+7(4)}{3+7},\frac{3(-3)+7(1)}{3+7}\right)$ = (−310,2510,−210)$\left(\frac{-3}{10},\frac{25}{10},\frac{-2}{10}\right)$

12. G is the centroid of the triangle. So, D is the mid-point of BC.
    Then, the coordinates of D are (x2+x32,y2+y32,z2+z32).$\left(\frac{x_2+x_3}{2},\frac{y_2+y_3}{2},\frac{z_2+z_3}{2}\right).$
    Also, AB = AC, thus ABC is an isoceles triangle. Thus, G divides in the ratio 2:1.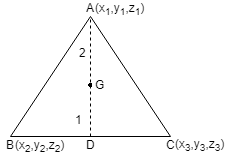
    
    Since, the centroid G divides AD in the ratio 2:1, then the coordinates of G are
    =[2⋅(x2+x32)+1⋅x12+1,2⋅(y2+y32)+1⋅y12+1$=[\frac{2\cdot \left(\frac{x_2+x_3}{2}\right)+1\cdot x_1}{2+1},\frac{2\cdot \left(\frac{y_2+y_3}{2}\right)+1\cdot y_1}{2+1}$2⋅(z2+z32)+1⋅z12+1]$\frac{2\cdot \left(\frac{z_2+z_3}{2}\right)+1\cdot z_1}{2+1}]$   [∵ Coordinates of internal division =(m1x2+m2x1m1+m2,m1y2+m2y1m1+m2,m1z2+m2z1m1+m2)]$\left[\begin{array}{l}\because \text{ Coordinates of internal division =}\\ \left(\frac{m_1{x}_2+m_2{x}_1}{m_1+m_2},\frac{m_1{y}_2+m_2{y}_1}{m_1+m_2},\frac{m_1{z}_2+m_2{z}_1}{m_1+m_2}\right)\end{array}\right]$
    
    =[x1+x2+x33,y1+y2+y33,z1+z2+z33]$=\left[\frac{x_1+x_2+x_3}{3},\frac{y_1+y_2+y_3}{3},\frac{z_1+z_2+z_3}{3}\right]$

13. Let a point P(x, y, z) such that PA + PB = 10
    
    ⇒(x−4)2+(y−0)2+(z−0)2−−−−−−−−−−−−−−−−−−−−−−−√$\Rightarrow \sqrt{(x-4{)}^2+(y-0{)}^2+(z-0{)}^2}$+(x+4)2+(y−0)2+(z−0)2−−−−−−−−−−−−−−−−−−−−−−−√=10$+\sqrt{(x+4{)}^2+(y-0{)}^2+(z-0{)}^2}=10$
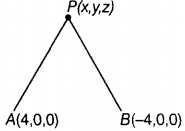
    [∵$\because$ distance =(x1−x2)2+(y1−y2)2+(z1−z2)2−−−−−−−−−−−−−−−−−−−−−−−−−−−−√]$=\sqrt{{\left(x_1-x_2\right)}^2+{\left(y_1-y_2\right)}^2+{\left(z_1-z_2\right)}^2}]$
    ⇒x2−8x+16+y2+z2−−−−−−−−−−−−−−−−−−√$\Rightarrow \sqrt{x^2-8x+16+y^2+z^2}$+x2+8x+16+y2+z2−−−−−−−−−−−−−−−−−−√=10$+\sqrt{x^2+8x+16+y^2+z^2}=10$
    ⇒x2+y2+z2−8x+16−−−−−−−−−−−−−−−−−−√$\Rightarrow \sqrt{x^2+y^2+z^2-8x+16}$=10−x2+y2+z2+8x+16−−−−−−−−−−−−−−−−−−√$=10-\sqrt{x^2+y^2+z^2+8x+16}$
    On squaring sides, we get
    x2 + y2 + z2 - 8x +16 = 100 + x2 + y2 + z2 + 8x +16
    −20x2+y2+z2+8x+16−−−−−−−−−−−−−−−−−−√$-20\sqrt{x^2+y^2+z^2+8x+16}$
    ⇒−16x−100=−20x2+y2+z2+8x+16−−−−−−−−−−−−−−−−−−√$\Rightarrow -16x-100=-20\sqrt{x^2+y^2+z^2+8x+16}$
    ⇒4x+25=5x2+y2+z2+8x+16−−−−−−−−−−−−−−−−−−√$\Rightarrow 4x+25=5\sqrt{x^2+y^2+z^2+8x+16}$ [dividing both sides by -4]
    Again squaring on both sides, we get
    16x2 + 200x + 625 = 25(x2 + y2 + z2 + 8x + 16)
    ⇒$\Rightarrow$ 16x2 + 200x + 625 = 25x2 + 25y2 + 25z2 + 200x + 400
    ⇒$\Rightarrow$ 9x2 + 25y2 + 25z2 - 225 =0

14. Let A (2, 0, 3), B(0, 3, 2) and C(0, 0, 1) be given points.
    Let P (x, y, 0) be any point in XY plane such that PA = PB = PC.
    Now PA = PB ⇒$\Rightarrow$ PA2 = PB2
    ∴$\therefore$ (x - 2)2 + (y - 0)2 + (0-3)2 = (x - 0)2 + (y - 3)2 + (0-2)2
    ⇒$\Rightarrow$4x - 6y =0 ⇒$\Rightarrow$ 2x - 3y = 0. . . (i)
    Also PB = PC ⇒$\Rightarrow$ PB2 = PC2
    ∴$\therefore$ (x - 0)2 + (y - 3)2 + (0 - 2)2 = (x - 0)2 + (y - 0)2 + (0 - 1)2
    ⇒$\Rightarrow$ x2 + y2 + 9 - 6y + 4 = x2 + y2 + 1
    ⇒$\Rightarrow$ 6y = 12 ⇒$\Rightarrow$ y = 2
    Putting value of y in (i), we have
    2x - 3 × 2 = 0 ⇒$\Rightarrow$ x = 3
    Thus coordinates of required point are (3, 2, 0).

15. Let A (-2, 6, -2), B(0, 4, -1), C(-2, 3, 1) and D (-4, 5, 0) be the given points. We have,
    
    AB=(0+2)2+(4−6)2+(−1+2)2−−−−−−−−−−−−−−−−−−−−−−−−√$AB=\sqrt{(0+2{)}^2+(4-6{)}^2+(-1+2{)}^2}$
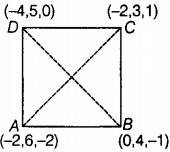
    [∵$\because$ distance = (x2−x1)2+(y2−y1)2+(z2−z1)2−−−−−−−−−−−−−−−−−−−−−−−−−−−−√$\sqrt{{\left(x_2-x_1\right)}^2+{\left(y_2-y_1\right)}^2+{\left(z_2-z_1\right)}^2}$]
    =4+4+1−−−−−−−√=9–√=3$=\sqrt{4+4+1}=\sqrt{9}=3$
    BC=(−2−0)2+(3−4)2+(1+1)2−−−−−−−−−−−−−−−−−−−−−−−−√$BC=\sqrt{(-2-0{)}^2+(3-4{)}^2+(1+1{)}^2}$
    =4+1+4−−−−−−−√=9–√=3$=\sqrt{4+1+4}=\sqrt{9}=3$
    CD=(−4+2)2+(5−3)2+(0−1)2−−−−−−−−−−−−−−−−−−−−−−−−√$CD=\sqrt{(-4+2{)}^2+(5-3{)}^2+(0-1{)}^2}$
    =4+4+1−−−−−−−√=9–√=3$=\sqrt{4+4+1}=\sqrt{9}=3$
    AD=(−4+2)2+(5−6)2+(0+2)2−−−−−−−−−−−−−−−−−−−−−−−−√$AD=\sqrt{(-4+2{)}^2+(5-6{)}^2+(0+2{)}^2}$
    =4+1+4−−−−−−−√=9–√=3$=\sqrt{4+1+4}=\sqrt{9}=3$
    Since, AB = BC = CD = DA. So, ABCD is a square or a rhombus.
    Now, AC=(−2+2)2+(3−6)2+(1+2)2−−−−−−−−−−−−−−−−−−−−−−−−√$AC=\sqrt{(-2+2{)}^2+(3-6{)}^2+(1+2{)}^2}$
    [∵$\because$ distance =(x2−x1)2+(y2−y1)2+(z2−z1)2−−−−−−−−−−−−−−−−−−−−−−−−−−−−√]$\sqrt{{\left(x_2-x_1\right)}^2+{\left(y_2-y_1\right)}^2+{\left(z_2-z_1\right)}^2}]$
    =0+9+9−−−−−−−√=18−−√$=\sqrt{0+9+9}=\sqrt{18}$
    and BD=(−4−0)2+(5−4)2+(0+1)2−−−−−−−−−−−−−−−−−−−−−−−−√$BD=\sqrt{(-4-0{)}^2+(5-4{)}^2+(0+1{)}^2}$
    =16+1+1−−−−−−−−√$=\sqrt{16+1+1}$
    =18−−√$=\sqrt{18}$
    Since, diagonal AC = diagonal BD
    Hence, ABCD is a square.