Sets - Test Papers

 CBSE Test Paper 01

CH-01 Sets

---

 

1. Section A

2. Let U be the universal containing 700 elements. If A and B are subsets of U such that n(A) = 200, n(B) = 300 and n(A∩B)=100$n(A\cap B)=100$then n(A′∩B′)=....$n(A^{\prime }\cap B^{\prime })=....$

   1. 400

   2. 300

   3. 500

   4. 800

3. If A = { 1,2,3,4 } , B = { 4,5,6,7 } ,A∩B=$A\cap B=$

   1. { 4 }

   2. { 1,2,3,4 }

   3. { 6 , 7 }.

   4. { 1, 2 }

4. If n (A ) =3 and n ( B ) = 6 and A⊆$\subseteq$ B , then n(A∪B)=?$n(A\cup B)=?$

   1. 9

   2. 3

   3. 6

   4. none of these

5. The number of proper subsets of the set { 1, 2 , 3 } is :

   1. 6

   2. 7

   3. 8

   4. 5

6. If A class has 175 students . The following data shows the number of students offering one or more subjects. Mathematics 100 ; Physics 70 ; Chemistry 40 ; Mathematics and Physics 30 ; Mathematics and Chemistry 28 ; Physics and Chemistry 23 ; Mathematics , Physics and Chemistry 18 . How many students have offered Mathematics alone?

   1. 35

   2. 22.

   3. 48

   4. 60

7. Fill in the blanks:

   If A = {1, 3, 5, 7, 9} and B = {2, 3, 5, 7, 11}, then AΔ$\mathrm{\Delta }$B is ________.

8. Fill in the blanks:

   A set, consisting of a single element, is called a ________.

9. List all the elements of set {x : x is a month of a year not having 31 days}.

10. State whether the statement is true or false: {a, e, i, o, u) and {a, b, c, d} are disjoint sets.

11. If U = {a, b, c, d, e, f, g, h}, find the complement of the set: D = {f, g, h, a}

12. Let A = {1, 2, 4, 5} B = {2, 3, 5, 6} C = {4, 5, 6, 7}. Verify:A−(B∪C)=(A−B)∩(A−C)$A-(B\cup C)=(A-B)\cap (A-C)$

13. If A is any set, prove that: A⊆ϕ⇔A=ϕ$A\subseteq \varphi \iff A=\varphi$

14. In a survey of 60 people, it was found that 25 people read newspaper H, 26 read newspaper T, 26 read newspaper I, 9 read both H and I, 11 read both H and T, 8 read both T and I, 3 read all three newspapers.
    Find: the number of people who read at least one of the newspaper.

15. For any two sets A and B prove that: P(A∩B)=P(A)∩P(B).$P(A\cap B)=P(A)\cap P(B).$

16. If U = {a, b, c, d, e, f} , A = {a, b,c}, B = {c, d, e, f} , C = {c, d, e} and D = {d, e, f}, then tabulate the following sets:

    1. A ∩$\cap$ D
    2. A ∩$\cap$ C
    3. U ∩$\cap$ D
    4. A∪ϕ$A\cup \varphi$
    5. (U∩ϕ$U\cap \varphi$)'
    6. (U ∪$\cup$ A)'

CBSE Test Paper 01
CH-01 Sets

---

Solution
Section A

1. (b) 300
   Explanation:
   Given n(A) = 200, n(B) =\ 300, n(A∩B)=100$n(A\cap B)=100$ 

   n(A∪B)=n(A)+n(B)−n(A∩B)$n(A\cup B)=n(A)+n(B)-n(A\cap B)$= 200 + 300 - 100 = 400

   n(A′∩B′)=n(A∪B)′+n(U)−n(A∪B)$n(A^{\prime }\cap B^{\prime })=n(A\cup B{)}^{\prime }+n(U)-n(A\cup B)$= 700 - 400 = 300
   [By De morgans law]

2. (a) { 4 }
   Explanation: Given A=1,2,3,4  and B=4,5,6,7
   (A∩B)={4}$(A\cap B)=\{4\}$
3. (c) 6
   Explanation:A⊆B$A\subseteq B$

    ⇒n(A∪B)=n(B)=6$\Rightarrow n(A\cup B)=n(B)=6$

4. (b) 7
   Explanation: The no of proper subsets=2n-1=23-1=7
   Here n=no of elements of given set=3
5. (d) 60
   Explanation:
   M -mathematics
   P - physics
   C - chemistry
   Venn Diagram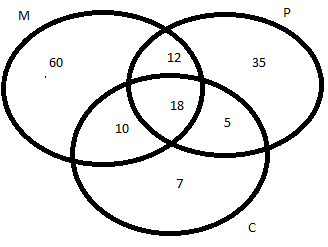

   
   By Venn Diagram we can see that the students who offered mathematics alone are 60.

6. {1, 2, 9, 11}

7. singleton set

8. A month has either 28, 29, 30 or 31 days.
   Out of the 12 months in a year, the months that have 31 days are:
   January, March, May, July, August, October, December
   ∴$\therefore$ Given set has elements {February, April, June, September, November}

9. Let A = {a, e, i, o, u} and B ={a, b, c, d}
   Now A∩B={a,e,i,o,u}∩{a,b,c,d}$A\cap B=\{a,e,i,o,u\}\cap \{a,b,c,d\}$= {a}
   Hence A and B are not disjoint. So the statement is false.

10.  D′=U−D={a,b,c,d,e,f,g,h}−{f,g,h,a}$D^{\prime }=U-D=\{a,b,c,d,e,f,g,h\}-\{f,g,h,a\}$={b, c, d, e}

11. A = {1,2,4,5}, B = {2,3,5,6}, C = {4,5,6,7}
    B∪C$B\cup C$= {2,3,4,5,6,7}
    A−(B∪C)$A-(B\cup C)$= {1} .....(i)
    (A - B) = { 1, 4}
    (A - C) = {1, 2}
    (A−B)∩(A−C)$(A-B)\cap (A-C)$= {1} .......(ii)
    From eqn (i) and eqn (ii), we get
    A−(B∪C)=(A−B)∩(A−C)$A-(B\cup C)=(A-B)\cap (A-C)$

12. The symbol '⇔$\iff$' stands for if and only if (in short if).
    In order to show that two sets A and B are equal, we show that A⊆B$A\subseteq B$ and B⊆A.$B\subseteq A.$
    We have A⊆ϕ,∵ϕ$A\subseteq \varphi ,\because \varphi$is a subset of every set,
    ∴ϕ⊆A$\therefore \varphi \subseteq A$
    Hence A = ϕ$\varphi$
    To show the backward implication, suppose that A=ϕ.$A=\varphi .$
    ∵$\because$ every set is a subset of itself
    ∴ϕ=A⊆ϕ$\therefore \varphi =A\subseteq \varphi$
    Hence, proved.

13. Here
    n(U) = a + b + c + d + e + f + g + h = 60 ....... (i)
    n (H) = a + b + c +d = 25 ....... (ii)
    n(T) = b + c + f + g = 26 ........ (iii)
    n(I) = c + d + e + f = 26 ....... (iv)
    n(H∩I)=c+d=9$n(H\cap I)=c+d=9$....... (v)
    n(H∩T)=b+c=11$n(H\cap T)=b+c=11$....... (vi)
    n(T∩I)=c+f=8$n(T\cap I)=c+f=8$....... (vii)
    n(H∩T∩I)=c=3$n(H\cap T\cap I)=c=3$....... (viii)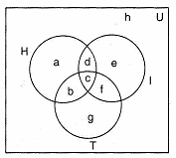
    
    Putting value of c in (vii),
    3+ f = 8 ⇒$\Rightarrow$ f = 5
    Putting value of c in (vi),
    3 +b = 11 ⇒$\Rightarrow$ b = 8
    Putting values of c in (v),
    3 + d = 9 ⇒$\Rightarrow$ d = 6
    Putting value of c, d, f in (iv),
    3 + 6 + e + 5 = 26 ⇒$\Rightarrow$e = 26 - 14 = 12
    Putting value of b, c, f in (iii),
    8 + 3 + 5 + g = 26 ⇒$\Rightarrow$ g = 26 - 16 = 10
    Putting value of b, c, d in (ii)
    a + 8 + 3 + 6 = 25 ⇒$\Rightarrow$ a = 25 - 17 = 8
    Number of people who read at least one of the three newspapers
    = a + b + c + d +e + f + g
    = 8 + 8 + 3 + 6 + 12 + 5 + 10 = 52

14. Let x∈P(A∩B)$x\in P(A\cap B)$
    ⇒x⊂(A∩B)$\Rightarrow x\subset (A\cap B)$
    ⇒x⊂A$\Rightarrow x\subset A$ and x⊂B$x\subset B$
    ⇒x∈P(A)$\Rightarrow x\in P(A)$ and x∈P(B)$x\in P(B)$
    ⇒x∈P(A)∩P(B)$\Rightarrow x\in P(A)\cap P(B)$
    ⇒x⊂P(A)∩P(B)$\Rightarrow x\subset P(A)\cap P(B)$
    ∴P(A∩B)⊂P(A)∩P(B)$\therefore P(A\cap B)\subset P(A)\cap P(B)$. . . (i)
    Let x∈P(A)∩P(B)$x\in P(A)\cap P(B)$
    ⇒x∈P(A)$\Rightarrow x\in P(A)$ and x∈P(B)$x\in P(B)$
    ⇒x⊂A$\Rightarrow x\subset A$ and ⇒x⊂B$\Rightarrow x\subset B$
    ⇒x⊂A∩B$\Rightarrow x\subset A\cap B$
    ⇒x⊂P(A∩B)$\Rightarrow x\subset P(A\cap B)$
    ∴P(A)∩P(B)⊂P(A∩B)$\therefore P(A)\cap P(B)\subset P(A\cap B)$. . . . (ii)
    From (i) and (ii), we have
    P(A∪B)=P(A)∩P(B)$P(A\cup B)=P(A)\cap P(B)$

15. According to the question, we are given that,
    U = {a, b, c, d, e, f} , A = {a, b,c}, B = {c, d, e, f} , C = {c, d, e} and D = {d, e, f}

    1. A ∩$\cap$ D = {a, b,c} ∩$\cap$ {d, e, f} = ϕ$\varphi$
    2. A ∩$\cap$ C = {a, b, c} ∩$\cap$ {c, d, e} = {c}
    3. U ∩$\cap$ D = {a, b, c, d, e, f} ∩$\cap$ {d, e, f} = {d, e, f}
    4. A∪ϕ$A\cup \varphi$= {a, b, c} ∪$\cup$ {} = {a,b,c}
    5. U ∩ϕ$\cap \varphi$ = {a, b, c, d, e, f} ∩$\cap$ {} = ϕ$\varphi$
       (U∩ϕ$U\cap \varphi$)'
       = ϕ′${\varphi }^{\prime }$
       = U 
    6. U ∪$\cup$ A = {a, b, c, d, e, f} ∪$\cup$ {a, ,b, c}
       = {a, b, c, d, e, f}
       = U
       ∴$\therefore$ (U ∪$\cup$ A)' = ϕ