Sequences and Series - Test Papers

 CBSE Test Paper 01

CH-09 Sequences and Series

---

1. the ratio of first to the last of n A.m.’s between 5 and 35 is 1 : 4. The value of n is

   1. 9

   2. 11

   3. 10

   4. 19

2. All the terms in A.P., whose first term is a and common difference d are squared. A different series is thus formed. This series is a

   1. H.P.

   2. G.P.

   3. A.P.

   4. none of these

3. If A, G, H denote respectively the A.M., G.M. and H.M. between two unequal positive numbers, then

   1. A = GH

   2. A2=GH$A^2=GH$

   3. A=G2H$A=G^{2}H$

   4. G2=HA$G^2=HA$

4. The next term of the sequence 1, 1, 2, 4, 7, 13,…. Is

   1. 21

   2. 24

   3. none of these

   4. 19

5. The sum of all non-reducible fractions with the denominator 3 lying between the numbers 5 and 8 is

   1. 31

   2. 52

   3. 41

   4. 39

6. Fill in the blanks:
   The general term or nth term of G.P. is given by an = ________.
7. Fill in the blanks:
   The third term of a G.P. is 4, the product of the first five terms is ________.

8. Find the sum of first n terms and the sum of first 5 terms of the geometric series 1+23+49+−−−$1+\frac{2}{3}+\frac{4}{9}+---$

9. Find the 12th term of a G.P. whose 8th term is 192 and the common ratio is 2.

10. Find the sum of 20 terms of an AP, whose first term is 3 and last term is 57.

11. Find the sum to n terms of the sequence: log a, log ar, log ar2, ...

12. The nth term of an AP is 4n + 1. Write down the first four terms and the 18th term of an AP.

13. Find the sum to n terms in each of the series 11×2+12×3+13×4+…$\frac{1}{1\times 2}+\frac{1}{2\times 3}+\frac{1}{3\times 4}+\dots$

14. Find the sum to n terms in each of the series  52 + 62 + 72 + ..... + 202

15. If a and b are the roots x2 - 3x + p = 0 and c, d are roots of x2 - 12x + q = 0 where a, b, c, d form a G.P. Prove that (q + p):(q - p) = 17:15.

CBSE Test Paper 01
CH-09 Sequences and Series

---

Solution

1. (a) 9
   Explanation:

   the sequence is 5,A1,A2,.....An,35$5,A_1,A_2,.....A_n,35$
   here a=5 and b=35
   we know that, d=b−an+1=35−5n+1=30n+1$d=\frac{b-a}{n+1}=\frac{35-5}{n+1}=\frac{30}{n+1}$
   According to question, 
   A1An=14$\frac{A_1}{A_n}=\frac{1}{4}$
   ⇒a+da+nd=14$\Rightarrow \frac{a+d}{a+nd}=\frac{1}{4}$
   ⇒4a+4d=a+nd$\Rightarrow 4a+4d=a+nd$
   ⇒3a=d(n−4)$\Rightarrow 3a=d(n-4)$
   ⇒3×5=(30n+1)(n−4)$\Rightarrow 3\times 5=\left(\frac{30}{n+1}\right)(n-4)$
   ⇒(n+1)=2(n−4)$\Rightarrow (n+1)=2(n-4)$
   ⇒n+1=2n−8$\Rightarrow n+1=2n-8$
   ⇒n=9$\Rightarrow n=9$

2. (d) none of these
   Explanation: the series obtained will not follow rules of AP, GP and HP
3. (d) G2=HA$G^2=HA$
   Explanation:
   Given the numbers are a and b, then we have 
   A⋅M=A=a+b2,G⋅M=G=ab−−√$A\cdot M=A=\frac{a+b}{2},G\cdot M=G=\sqrt{ab}$  and H⋅M=H=2aba+b$H\cdot M=H=\frac{2ab}{a+b}$
   Now AH=(a+b2)(2aba+b)=ab=(ab−−√)2=G2$AH=\left(\frac{a+b}{2}\right)\left(\frac{2ab}{a+b}\right)=ab=(\sqrt{ab}{)}^2=G^2$
4. (b) 24
   Explanation:
   The given sequence can be expressed as T1=T2=1$T_1=T_2=1$
   Tn=Tn−1+Tn−2+Tn−3$T_n=T_{n-1}+T_{n-2}+T_{n-3}$, n≥3$n\ge 3$∴T7=T6+T5+T4=13+7+4=24$\therefore T_7=T_6+T_5+T_4=13+7+4=24$
5. (d) 39
   Explanation:
   We have 5=153 and 8=243$5=\frac{15}{3}\text{ and }8=\frac{24}{3}$
   Hence the fractions between5 and 8 with 3 as denominator will be 163,173,183,193,203,213,223$\frac{16}{3},\frac{17}{3},\frac{18}{3},\frac{19}{3},\frac{20}{3},\frac{21}{3},\frac{22}{3}$ and 233$\frac{23}{3}$ in this only 6=183$6=\frac{18}{3}$ and 7=213$7=\frac{21}{3}$ are reducible
   Now 163,173,183,193,203,213,223$\frac{16}{3},\frac{17}{3},\frac{18}{3},\frac{19}{3},\frac{20}{3},\frac{21}{3},\frac{22}{3}$and 233$\frac{23}{3}$ is an A.P with first term a = 163$\frac{16}{3}$ and d=13$d=\frac{1}{3}$
   Hence Sum =n2(a+l)=82(163+233)=4(13)=52$\frac{n}{2}(a+l)=\frac{8}{2}\left(\frac{16}{3}+\frac{23}{3}\right)=4(13)=52$
   Hence the sum of non redubile fractions = 52-(6+7)=52-13 = 39

6. arn-1

7. 45

8. a = 1, r = 23$\frac{2}{3}$
   Sn=a(1−rn)1−r$S_n=\frac{a\left(1-r^n\right)}{1-r}$
   =1[1−(23)n]1−23$=\frac{1\left[1-{\left(\frac{2}{3}\right)}^n\right]}{1-\frac{2}{3}}$
   =3[1−(23)n]$=3\left[1-{\left(\frac{2}{3}\right)}^n\right]$
   S5=3[1−(23)5]=21181$S_5=3\left[1-{\left(\frac{2}{3}\right)}^5\right]=\frac{211}{81}$

9. Let a be the first term of given G.P. Here r =2 and a8 = 192
   ∴$\therefore$an = arn-1
   ⇒a8=a×(2)8−1=192$\Rightarrow a_8=a\times (2{)}^{8-1}=192$
   ⇒a×(2)7=192$\Rightarrow a\times (2{)}^7=192$
   ⇒a×128=192$\Rightarrow a\times 128=192$
   ⇒a=192128=32$\Rightarrow a=\frac{192}{128}=\frac{3}{2}$
   ∴$\therefore$a12 = ar12 - 1
   ⇒a12=32×211=3×210$\Rightarrow a_{12}=\frac{3}{2}\times 2^{11}=3\times 2^{10}$
   = 3 ×$\times$1024 = 3072

10. We have, a = 3, l = 57 and n = 20
    ∵$\because$ Sn = n2$\frac{n}{2}$ [a + l]
    ∴$\therefore$ S20 = 202$\frac{20}{2}$ [3 + 57]
    = 10 ×$\times$ 60
    = 600

11. We have sequence log a, log ar, log ar2, ...
    Above sequence can be expressed as log a, (log a + log r), (log a + 2 log r), ...
    [∵$\because$ log mn = log m + log n and log nr = r log n]
    which is clearly an AP with, a = log a and d = log r
    We know that, sum of n terms,
    Sn = n2$\frac{n}{2}$ [2a + (n - 1)d]
    ∴$\therefore$ Sn = n2$\frac{n}{2}$ [2 log a + (n - 1) log r]
    = n2$\frac{n}{2}$ [log a2 + log rn-1] [∵$\because$x log a = log ax]
    = n2$\frac{n}{2}$ [log a2rn-1] [∵$\because$ log a + log b = log ab]

12. Here, Tn = 4n + 1 ...(i)
    On putting n = 1, 2, 3, 4 in Eq. (i), we get
    T1 = 4(1) + 1 = 4 + 1 = 5
    T2 = 4 (2) + 1 = 8 + 1 = 9
    T3 = 4 (3) + 1 = 12 + 1 = 13
    and T4 = 4 (4) + 1 = 16 + 1 = 17
    On putting n = 18 in Eq. (i), we get
    T18 = 4(18) + 1 = 72 + 1 = 73
    Hence, the first four terms of an AP are 5, 9, 13, 17 and 18th term is 73.

13. Given: 11×2+12×3+13×4+………$\frac{1}{1\times 2}+\frac{1}{2\times 3}+\frac{1}{3\times 4}+\dots \dots \dots$ to n terms

    ∴an=1(nthterm of 1,2,3,......)(nthterm of 2,3,4,.......)$\therefore a_n=\frac{1}{\left(n^{th}termof1,2,3,......\right)\left(n^{th}termof2,3,4,.......\right)}$

    =1[1+(n−1)×1][2+(n−1)×1]$=\frac{1}{[1+(n-1)\times 1][2+(n-1)\times 1]}$

    Let 1n(n+1)=An+Bn+1$\frac{1}{n(n+1)}=\frac{A}{n}+\frac{B}{n+1}$ [By partial fraction]

    Then 1=A(n+1) + Bn

    Put n=0 then A=1

    Put n=-1 then B=-1

    ∴$\therefore$1n(n+1)=1n+−1n+1$\frac{1}{n(n+1)}=\frac{1}{n}+\frac{-1}{n+1}$

    ∴a1=11−12a2=12−13a3=13−14$\therefore a_1=\frac{1}{1}-\frac{1}{2}{a}_2=\frac{1}{2}-\frac{1}{3}{a}_3=\frac{1}{3}-\frac{1}{4}$.........

    And Sn = a1 + a2 + a3 + ........ + an

    =11−1n+1=nn+1$=\frac{1}{1}-\frac{1}{n+1}=\frac{n}{n+1}$

14. Given: 52 + 62 + 72 + ....... + 202

    = (12 + 22 + 32 + ...... + 202) - (12 + 22 + 32 + 42)

    ∑n=120n2−∑n=14n2$\sum _{n=1}^{20}{n}^2-\sum _{n=1}^4{n}^2$

    =20(20+1)(40+1)6−4(4+1)(8+1)6$=\frac{20(20+1)(40+1)}{6}-\frac{4(4+1)(8+1)}{6}$

    =20×21×416−20×96$=\frac{20\times 21\times 41}{6}-\frac{20\times 9}{6}$

    =206(861−9)=2840$=\frac{20}{6}(861-9)=2840$

15. Let ba=cb=dc=k$\frac{b}{a}=\frac{c}{b}=\frac{d}{c}=k$ 

    ∴ba=k$\therefore \frac{b}{a}=k$

    ⇒$\Rightarrow$ b = ak And cb=k$\frac{c}{b}=k$

    ⇒$\Rightarrow$ c = bk = (ak)k = ak2 

    Also dc=k$\frac{d}{c}=k$

    ⇒$\Rightarrow$ d = ck = (ak2)k = ak3

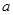    ∵$\because$  a and b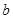 are the roots x2 - 3x + p = 0 

    ∴a+b=−(−3)1=3$\therefore a+b=\frac{-(-3)}{1}=3$  

    ⇒$\Rightarrow$ a + ak = 3

    ⇒$\Rightarrow$ a(1 + k) = 3  ……….(i)

    And ab=p1$ab=\frac{p}{1}$

    ⇒$\Rightarrow$ a(ak) = p

    ⇒$\Rightarrow$ a2k = p​ ......(ii)

    Also c, d are roots of x2 - 12x + q = 0 

    ∴c+d=−(−12)1=12$\therefore c+d=\frac{-(-12)}{1}=12$

    ⇒$\Rightarrow$ ak2 + ak3 = 12  

    ⇒$\Rightarrow$ ak2(1 + k) = 12 ……….(iii)

    And cd=q1$cd=\frac{q}{1}$

    ⇒$\Rightarrow$ ak2(ak3) = q

    ⇒$\Rightarrow$ a2k5 = q ……….(iv)

    Dividing eq. (iii) by eq. (i), ak2(1+k)a(1+k)=123$\frac{a{k}^2(1+k)}{a(1+k)}=\frac{12}{3}$   

    ⇒$\Rightarrow$ k2 = 4  

    ⇒k=±2$\Rightarrow k=\pm 2$

    Now q+pq−p=a2k5+a2ka2k5−a2k=a2k(k4+1)a2k(k4−1)$\frac{q+p}{q-p}=\frac{a^2{k}^5+a^{2}k}{a^2{k}^5-a^{2}k}=\frac{a^{2}k\left(k^4+1\right)}{a^{2}k\left(k^4-1\right)}$ 

    =(±2)4+1(±2)4−1=16+116−1=1715$=\frac{(\pm 2{)}^4+1}{(\pm 2{)}^4-1}=\frac{16+1}{16-1}=\frac{17}{15}$

    Therefore, (q + p):(q - p) = 17:15